Предмет: Математика,
автор: Vtesk
Пожалуйста объясните как решать это показательное уравнение
3^x+4+3*5^x+3=5^x+4+3^x+3
Приложения:
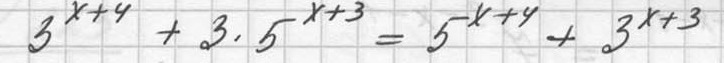
Vtesk:
ок
да, я понял что ты написал(а)
смотрю кинушку.. если никто не решит.. ответ скину сюда же в коммент попозже.. (может и решение оформлю, но вряд ли)
без проблем
просто с ходу: 3^(x+3)=5^(x+3), а отсюда х= -3
степени 3 выведи в одну сторону, а степени 5 в другую..
и вынеси за скобку в степени (х+3) для каждой стороны (три и пять)
если напишите НЕПОНЯТНО.. оформлю решение, но позже...
немного непонимаю
НЕПОНЯТНО
Ответы
Автор ответа:
0
разделим основания степеней
Ответ: х= - 3
перед строкой х+3=0, можно написать одну из строк или (3/5)^(x+3)=1 или (5/3)^(x+3)=1
сам ща напишу..
Похожие вопросы
Предмет: География,
автор: Dorizane
Предмет: Қазақ тiлi,
автор: lunevak23
Предмет: Английский язык,
автор: dima666228225
Предмет: Информатика,
автор: Ximikvrn
Предмет: Биология,
автор: Shmelewasasha