Помогите пожалуйста с решением этих неравенств
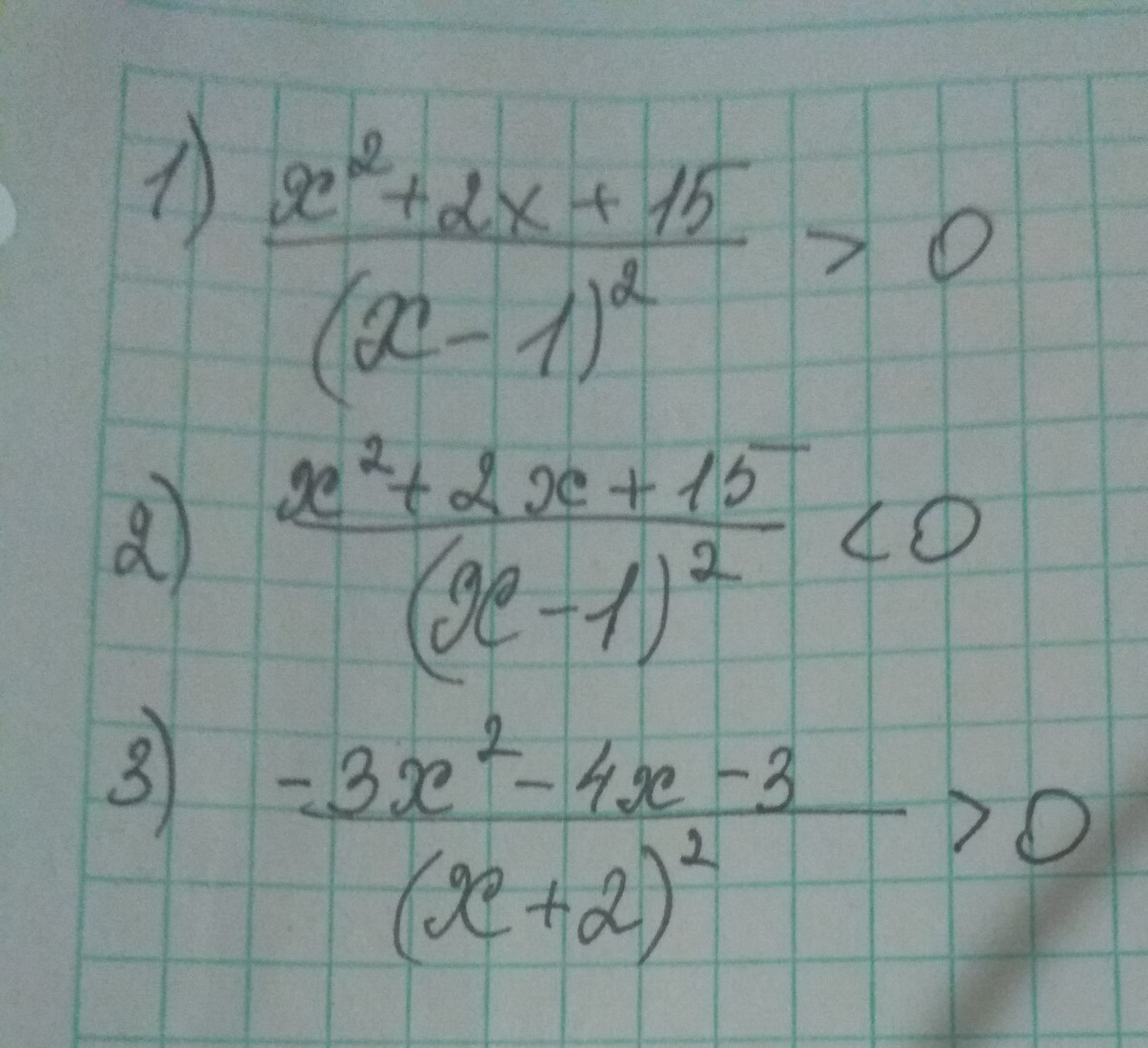
Ответы
D < 0 и a > 0 ⇒ числитель всегда положительное число.
(x-1)² тоже всегда положительное, осталось найти область определения.
x ∈ (-∞; 1) ∪ (1; ∞)
Мы знаем, что обе части положительны ⇒ x ∈ ∅
D < 0 и a < 0 ⇒ числитель всегда отрицательное число, знаменатель всегда положительное число ⇒ x ∈ ∅
Задание 1
, так как числитель не решается (D < 0), и по ОДЗ x ≠ 1, рисуем числовую прямую, на которой отмечаем точку 1 не выколотой. Так как скобка в знаменателе в квадрате, то знак при методе интервалов повторится.
+ 1 +
___________o_____________
То есть x принадлежит всей числовой оси, кроме 1.
Ответ
x ∈ R \ {1}
Задание 2
Аналогично с первым. Числитель не решается, и так как у нас скобка в знаменателе с квадратом, отмечаем одну точку и по методу интервалу определяем, где функция принимает отрицательные значения. (смотрим на числовую прямую, приведённую в 1 Задании) Как мы можем увидеть, значений, при которых бы функция была отрицательной нет.
Ответ
x ∉ R
Задание 3
. Вынесем знак минуса в числителе за скобку, получим
, домножим на -1 и получится
, так как числитель не решается (D < 0), и по ОДЗ x ≠ -2, рисуем числовую прямую, на которой отмечаем точку 2 не выколотой. Так как скобка в знаменателе в квадрате, то знак при методе интервалов повторится.
+ 2 +
_________o_________
Опять мы выходим на подобный второму заданию ответ, где x принадлежит всей числовой оси, кроме 2, так как не существует промежутков, при которых функция принимала бы отрицательное значение.
Ответ
x ∉ R