Предмет: Геометрия,
автор: dimon43168
Помогите решить 2 вариант все задания
Приложения:
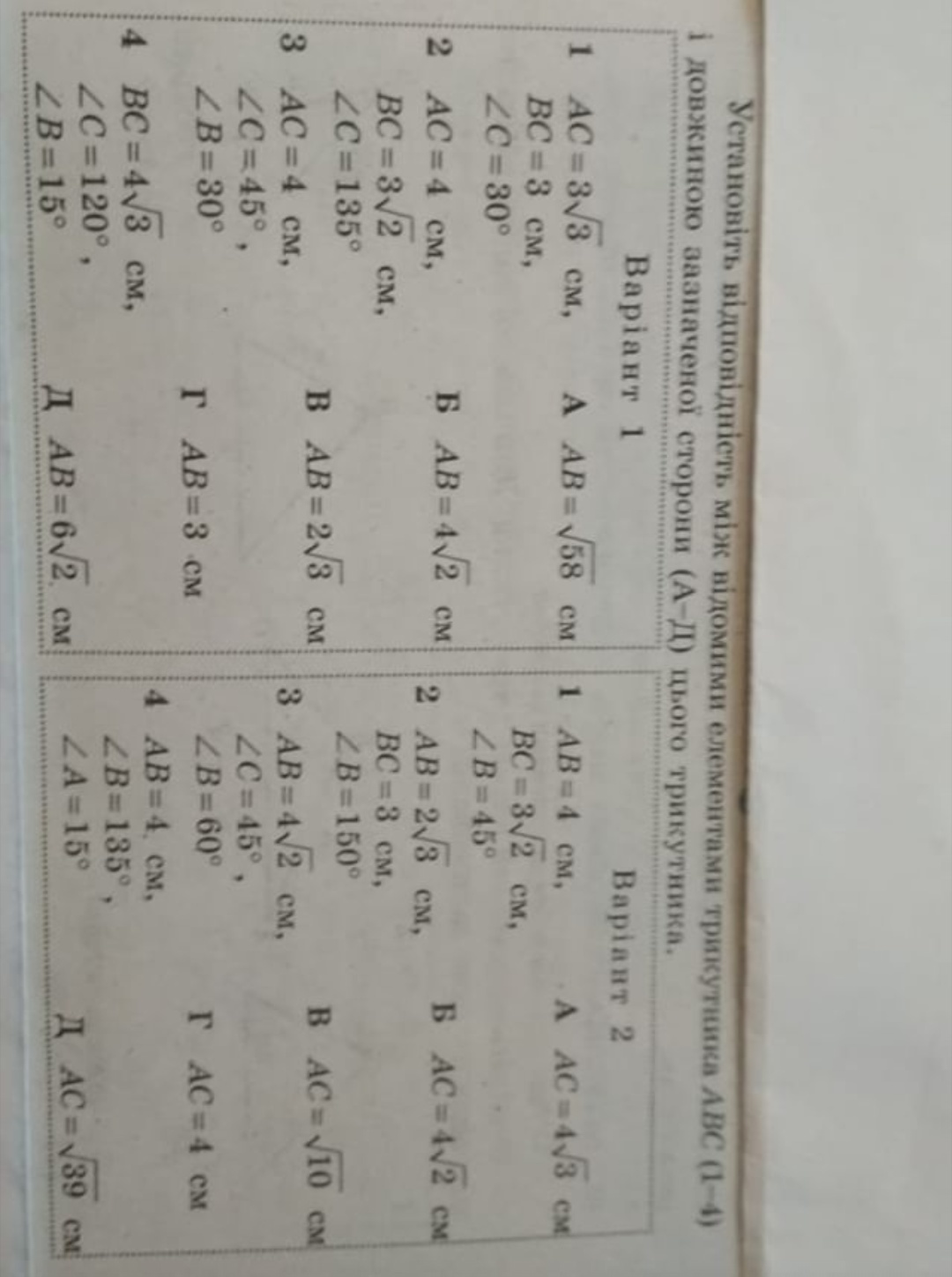
Ответы
Автор ответа:
1
По теореме косинусов:
По теореме синусов:
Похожие вопросы
Предмет: Русский язык,
автор: karkarich228
Предмет: Українська мова,
автор: vericmaria72
Предмет: География,
автор: hhgdsdj11
Предмет: Математика,
автор: міні23
Предмет: Математика,
автор: tomas633