Предмет: Математика,
автор: f19492
Помогите решить пожалуйста. С пояснением.
Приложения:
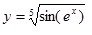
krolikzajcev:
Чё делать то?
Найти производную сложной функции
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Қазақ тiлi,
автор: bekabahtybaj30
Предмет: Українська мова,
автор: itsapikushad
Предмет: Геометрия,
автор: yuliyabagun
Предмет: Математика,
автор: vbkj5lbkArihka