Предмет: Математика,
автор: tsmajaylive
Выполнить потенцирование выражений:
1) log x = log 3 + log 5 - log 2
2) log x = 3log 5 + 2log 3
3) log x = 2log 13 - 2/5log 2 - 1/3log 7
4) log x = log (a+b) - 2/3(2log a + 3/4log b)
5) log x = 2log(a-b)+3/4(log a - 2/3log b)
Приложения:
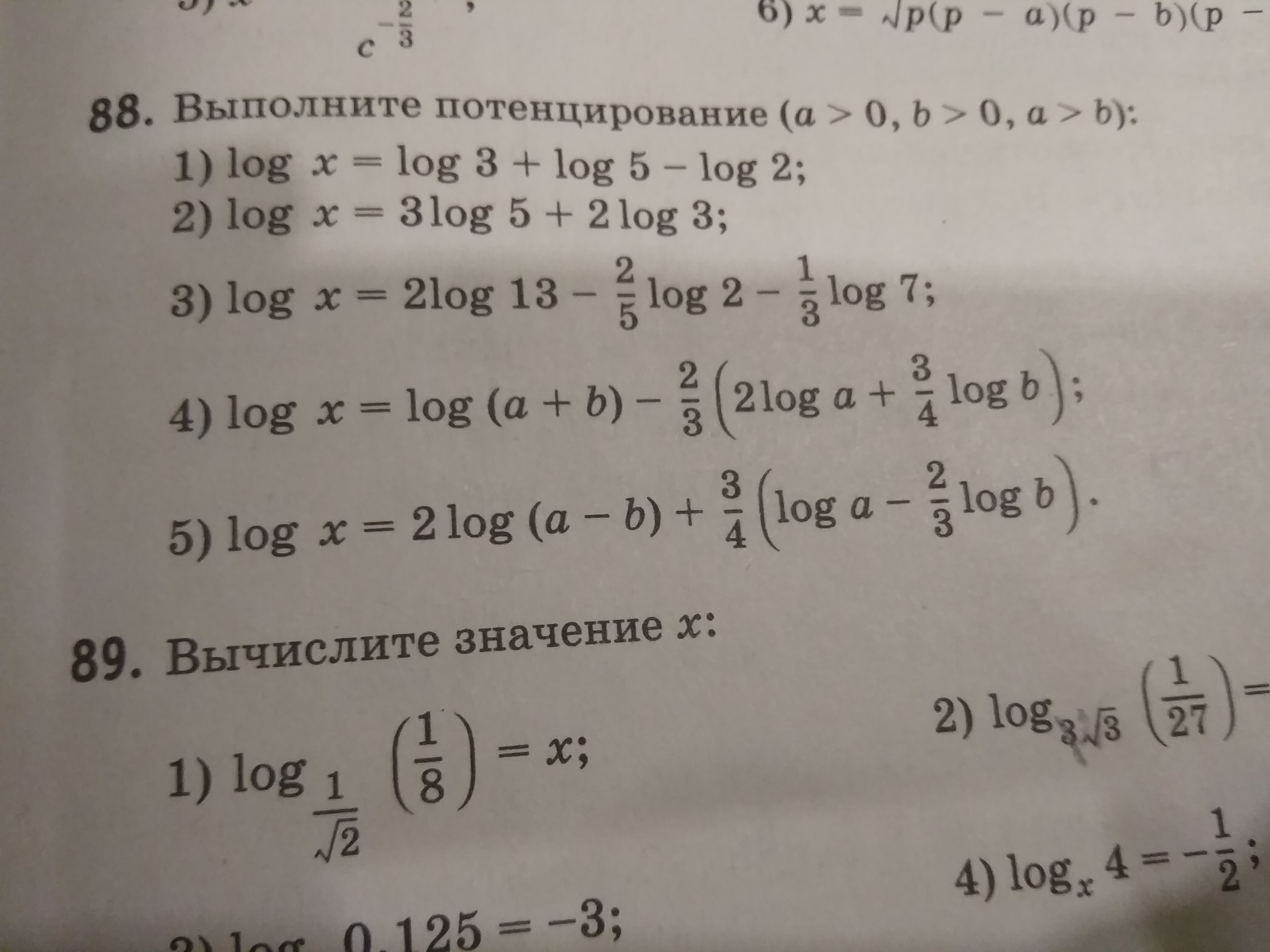
Ответы
Автор ответа:
6
Ответ:
Используем свойства логарифмов:
.
В задаче основания логарифмов не дано, поэтому будем считать одинаковыми!
Похожие вопросы
Предмет: Геометрия,
автор: ikoooonaa
Предмет: Математика,
автор: cukejccue
Предмет: Математика,
автор: asbideo
Предмет: Алгебра,
автор: ichmaelz
Предмет: Алгебра,
автор: Sofia1224