Предмет: Алгебра,
автор: Данякеп
Найти неопределенные интегралы. Результаты проверить дифференцированием.
Приложения:
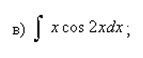
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Қазақ тiлi,
автор: askarnuraj422
Предмет: Литература,
автор: 3yukhu
Предмет: Українська мова,
автор: sandra92938
Предмет: Алгебра,
автор: mishenina98