Question

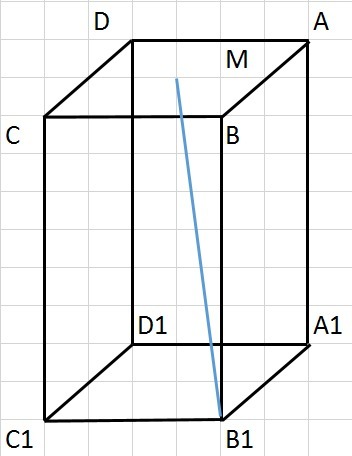
В паралелипипеде abcda1b1c1d1 точка М - середина грани abcd. Вычислить угол между прямыми b1m и cc1, если паралелипипед прямоугольный, в основании лежит квадрат, а длина бокового ребра в 2 раза больше стороны основания. 80 баллов. Нужны рисунок, подробное решение с доказательством каждого пункта действий.

Answer 1

$\vec {C_1B_1} = (1,0,0)\\\vec{C_1D_1}=(0,1,0)\\\vec{C_1C}=(0,0,2)\\\vec{B_1M}=\vec{B_1B}+\frac{1}{2}\vec{BA}-\frac{1}{2}\vec{DA}=(-0.5,0.5,2)\\\vec{B_1M}\times\vec{C_1C}=(-0.5,0.5,2)\times(0.0.2)=4\\\vec{B_1M}\times\vec{C_1C}=|\vec{B_1M}|*|\vec{C_1C}|*\cos \phi=\\=\sqrt{0.25+0.25+4}*2*\cos \phi\\\cos \phi=\frac{4}{2\sqrt{4.5}}=\frac{2\sqrt{2}}{3}\\\phi = \arccos{\frac{2\sqrt{2}}{3}}$