Question

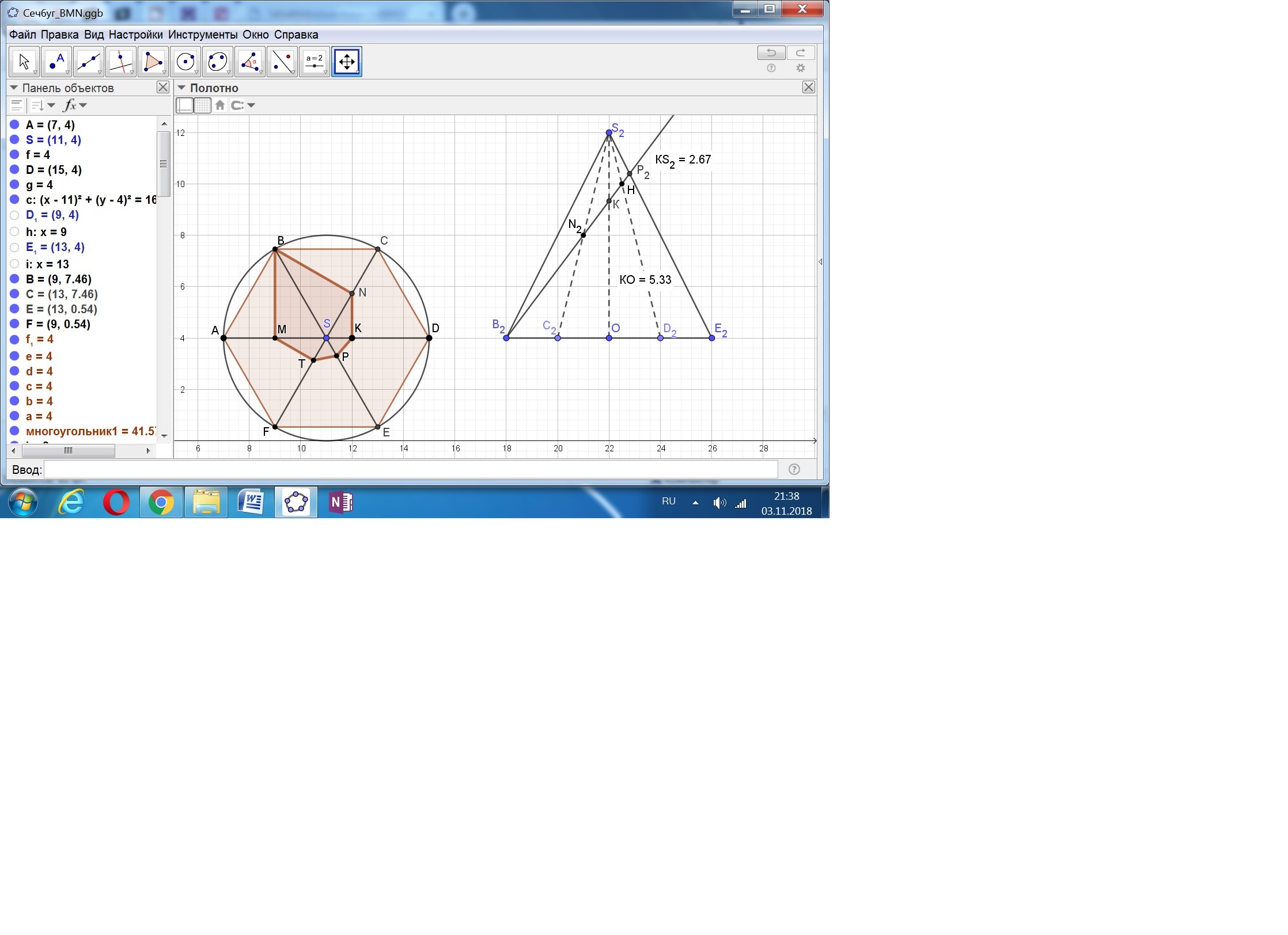
Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Точки M и N — середины рёбер SA и SC.
а) Постройте сечение пирамиды плоскостью, проходящей через
точки M, N и B.
б) В каком отношении плоскость сечения делит отрезок, соединяющий вершину S с центром основания пирамиды?

Answer 1

а) Сечение строится с использованием следа d, параллельного MN.

Затем до этой линии продлеваем стороны основания и через полученные точки и точки M и N проводим линии SD и SF.

Аналогично находим точку на ребре SE.

б) Деление высоты в точке К построенной плоскостью определяем по теореме Менелая. (SK/KO)*(2/1)*(1/1) = 1.

Отсюда (SK/KO) = (1/2).

Для этого используем сечение пирамиды плоскостью BSE, на которое проецируется ребро SC.

В этой проекции ВС = СО по свойству шестиугольника, CN = NS  по заданию.

Получаем треугольник CSO и секущая ВК.