Предмет: Алгебра,
автор: Довакин007
Решите уравнения методом приведения обеих частей уравнения к одному основанию:
1).
2).
3).![\sqrt[x]{3} * \sqrt[x]{5}=225 \sqrt[x]{3} * \sqrt[x]{5}=225](https://tex.z-dn.net/?f=%5Csqrt%5Bx%5D%7B3%7D+%2A+%5Csqrt%5Bx%5D%7B5%7D%3D225)
4).
5).![\sqrt[x]{256} =4^{x} \sqrt[x]{256} =4^{x}](https://tex.z-dn.net/?f=%5Csqrt%5Bx%5D%7B256%7D+%3D4%5E%7Bx%7D)
Ответы
Автор ответа:
0
x²-11x+30=2;
x²-11x+28=0;
D=121-4*28=9;
x₁=(11+3)/2=7;
x₂=(11-3)/2=4;
2)
3)
4)
5)
Автор ответа:
0
Я не решил 3 т.к отве СОРРИ
Приложения:
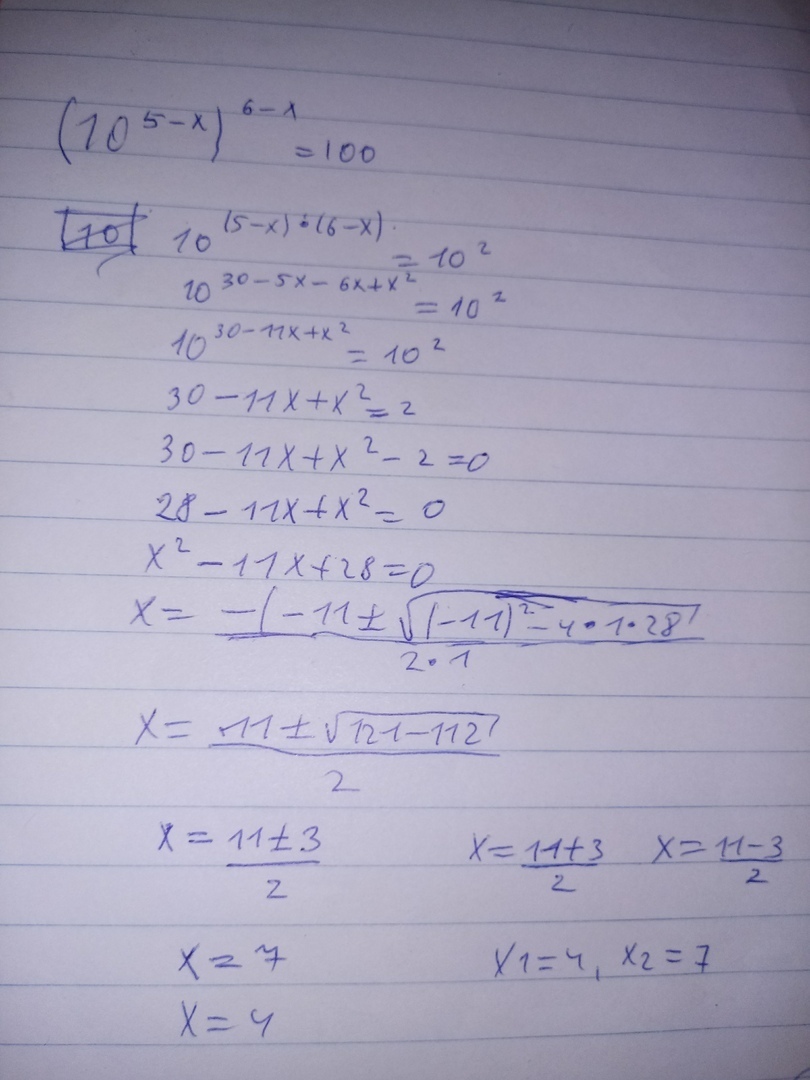
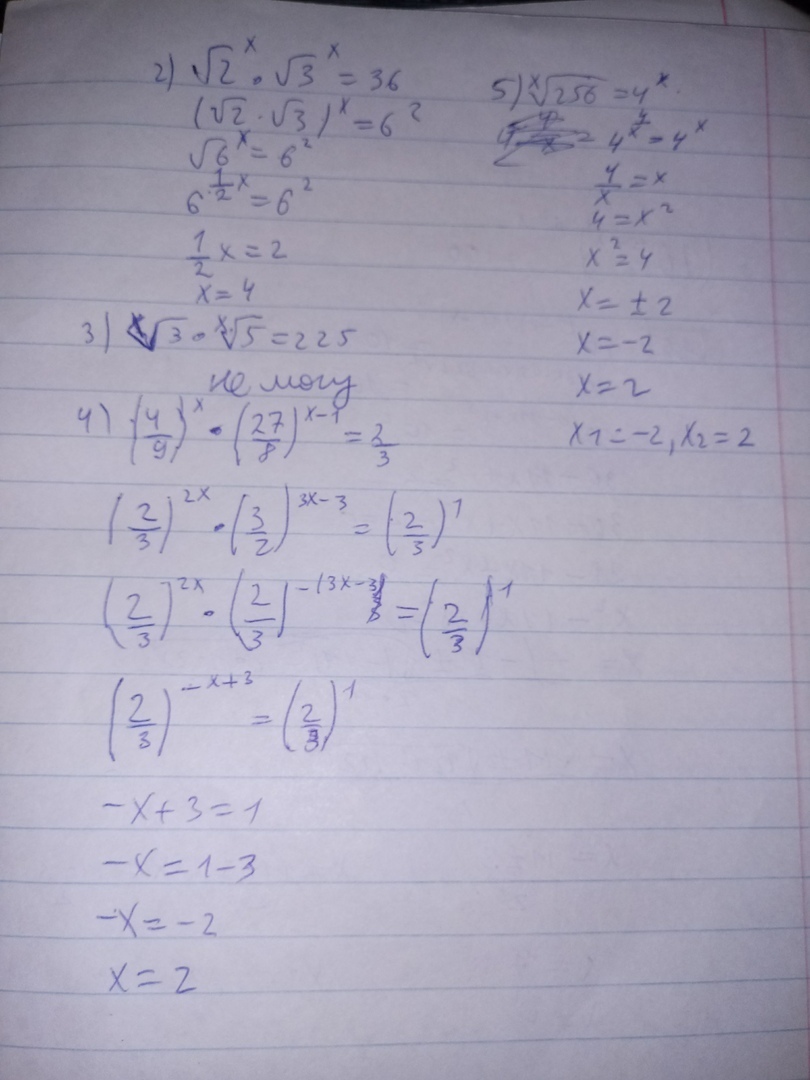
Похожие вопросы
Предмет: Физика,
автор: anastasiatalimoncuk
Предмет: Русский язык,
автор: erni031223
Предмет: Биология,
автор: Аноним
Предмет: Химия,
автор: kristinaalekse1
Предмет: Математика,
автор: KatyaZenit