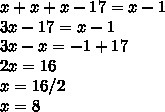Можно ли разрезать шахматную доску 8 на 8 на прямоугольники 1 на 2 так, чтобы остались только угловые клетки a1 и h8?
Назовите четырёхзначное число, у которого все цифры различны, и известно, что числа 5860, 1674, 9432, 3017 содержат ровно по две цифры, принадлежащие этому числу, однако ни одна из них не стоит в том же месте, что и в этом числе.
Угадайте значение xx в уравнении: x+x+x−17=x−1
Ответы
1. Нет, не получится. Представим, будто мы обкладываем поле доминошками. Каждая доминошка покрывает одно черное и одно белое поле, а при выкидывании полей a1 и h8 черных полей оказывается на 2 меньше, чем белых.
2. Решение Пусть искомое число abcd. Для каждой цифры a,b,c,d посчитаем, сколько раз она встречается в данных четырех числах. Очевидно, что сумма этих вхождений должна равняться 8. Поскольку никакая цифра не встречается в 3 числах, то каждая цифра встречается ровно дважды. Т.е. в искомом числе могут быть только цифры 0,1,3,4,6,7. Но в первом числе из этих цифр есть только 6 и 0. Значит, эти цифры в числе точно есть. Аналогично из третьего числа, получаем цифры 4 и 3. Составим табличку, в которой плюсики стоят в тех разрядах, в которых они могут быть написаны.
0 + − + −
3 − + − +
4 + − + −
6 + − − +
Т.к. в разряде сотен есть только один « + », то в разряде сотен числа стоит тройка. Действуя так далее и воспользовавшись тем, что четырехзначное число с нуля не начинается, получим число 4306, которое, очевидно, подходит. Ответ 4306.
3. решение в файле