Предмет: Математика,
автор: lipih
как это решить???помогите
Приложения:
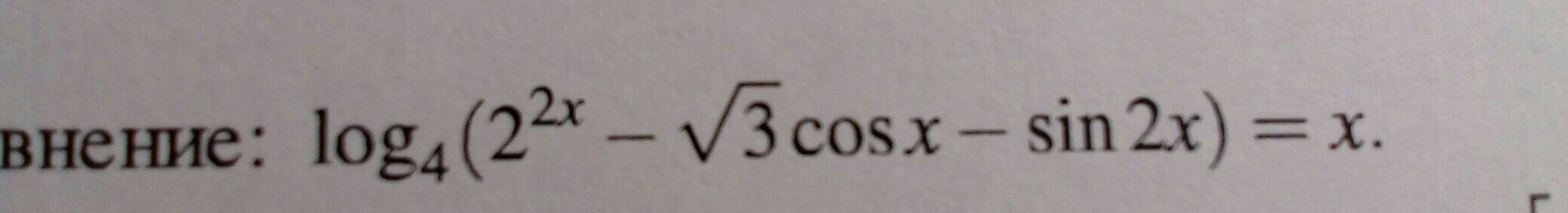
Ответы
Автор ответа:
0
И раз ответом является данное выражение, то функция на корнях всегда будет существовать, ведь на всей области определения
Похожие вопросы
Предмет: Русский язык,
автор: sofihorsee
Предмет: Физика,
автор: mellinanime
Предмет: Русский язык,
автор: aalvinna08
Предмет: Физика,
автор: Dayspisatplizz