Предмет: Алгебра,
автор: Аноним
Помогите!!!! 30 б!! На вас последняя надежда!
Приложения:
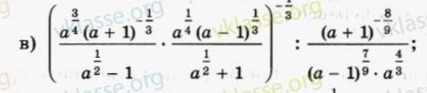
Ответы
Автор ответа:
2
смотри решение внизу.при решении применяем св-во степеней(найди их в учебнике)
Приложения:
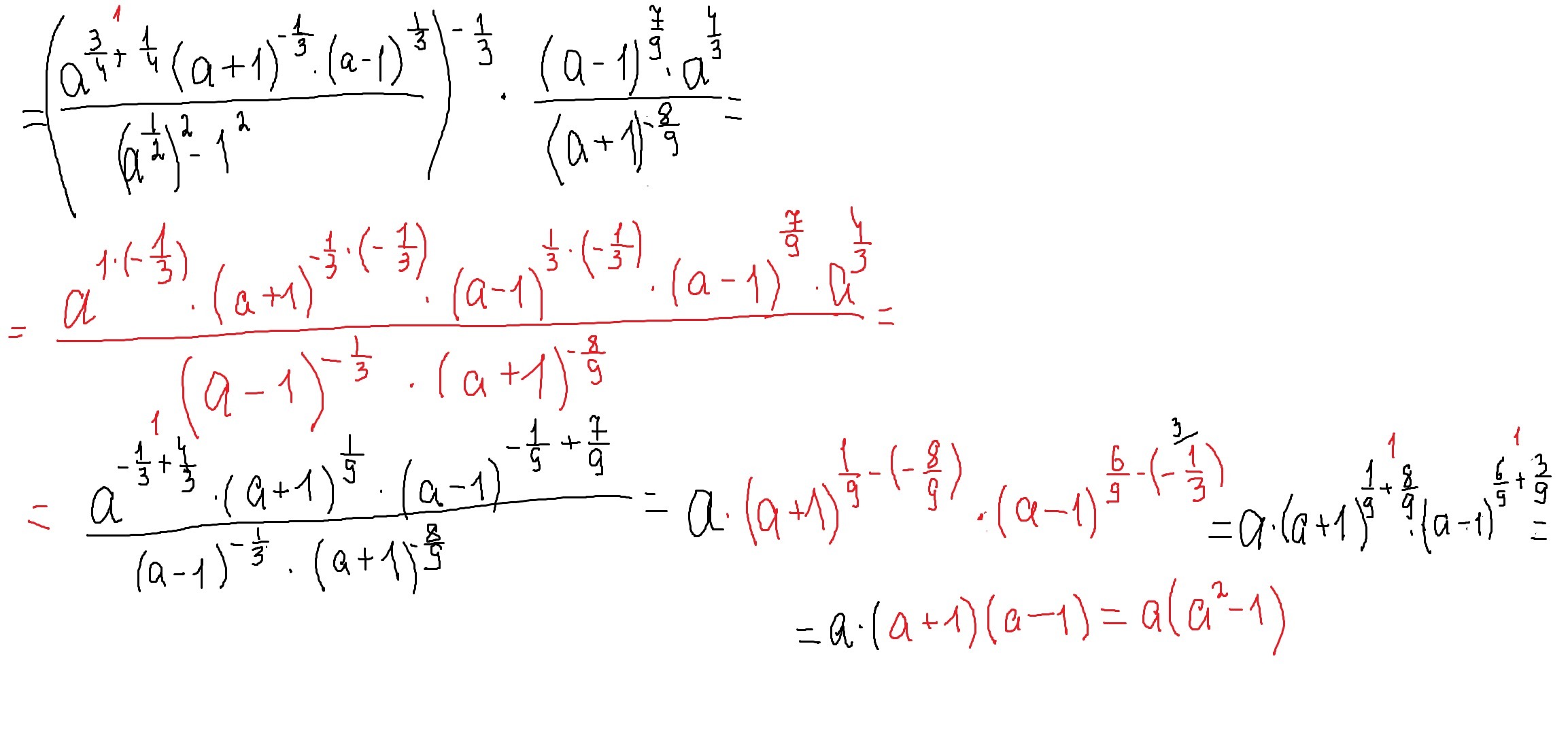
Аноним:
Огромное Вам спасибо!! Я болела-многое не понимала,так что Ваши рекомендации учту! Еще раз благодарю! Удачи Вам во всем!!
хоть в чем то разобралась?там вроде не сложно,только запись получается "страшная"э
Все ясно,кроме- (а-1) в-1\3 степени как получилось?
Автор ответа:
3
А как просто а получилось?
сложи 3/4+1/4=1 --> a^1=a
А нет все, поняла! Просто 2 часа ночи мысли путаются
поэтому ложись спать... А утро вечера мудренее...
Как раз собиралась,просто жду ответа на другое задание, может вы посмотрите https://znanija.com/task/29954169 ?
уже на завтра все дела, сама уже устала
Хорошо. Спасибо вам за решение! Отдыхайте)
Похожие вопросы
Предмет: Другие предметы,
автор: nikt1me
Предмет: Обществознание,
автор: Аноним
Предмет: Математика,
автор: violettagolynska
Предмет: Химия,
автор: КатяСухорукова
Предмет: Алгебра,
автор: Raymond2223