Предмет: Алгебра,
автор: Аноним
Номер 335 под буквой Б, упростите выражение
Приложения:
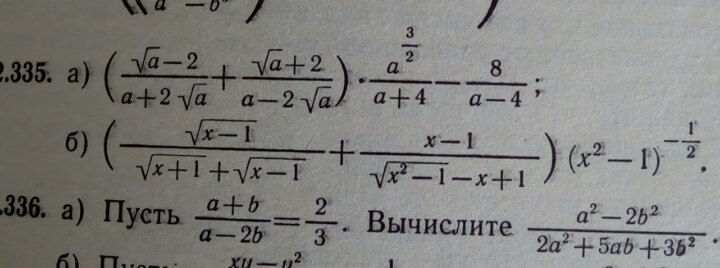
Ответы
Автор ответа:
1
решаем по действиям.
1) преобразуем первую дробь
2) выполним сложение
3) выполним умножение
Автор ответа:
4
task/29835486 см ПРИЛОЖЕНИЕ
Приложения:

vvvladgaio:
вот это класс вы лучший
Оганес вы король
Ошибайтесь , а вот Надежда настоящая КОРОЛЕВА
Спасибо) Ваше решение более рациональнее
Оганес, вы просто джентельмен, не хотите обидеть Надежду и хвалите ее, не надо скрывать все знаю что вы лучше ее!
Арифметика , не более (закончили)
Похожие вопросы