Предмет: Алгебра,
автор: noname479
Упростите выражение:

Ответы
Автор ответа:
1
Автор ответа:
1
Решение задания приложено. На втором листочке, если всё - таки бетта.
Приложения:
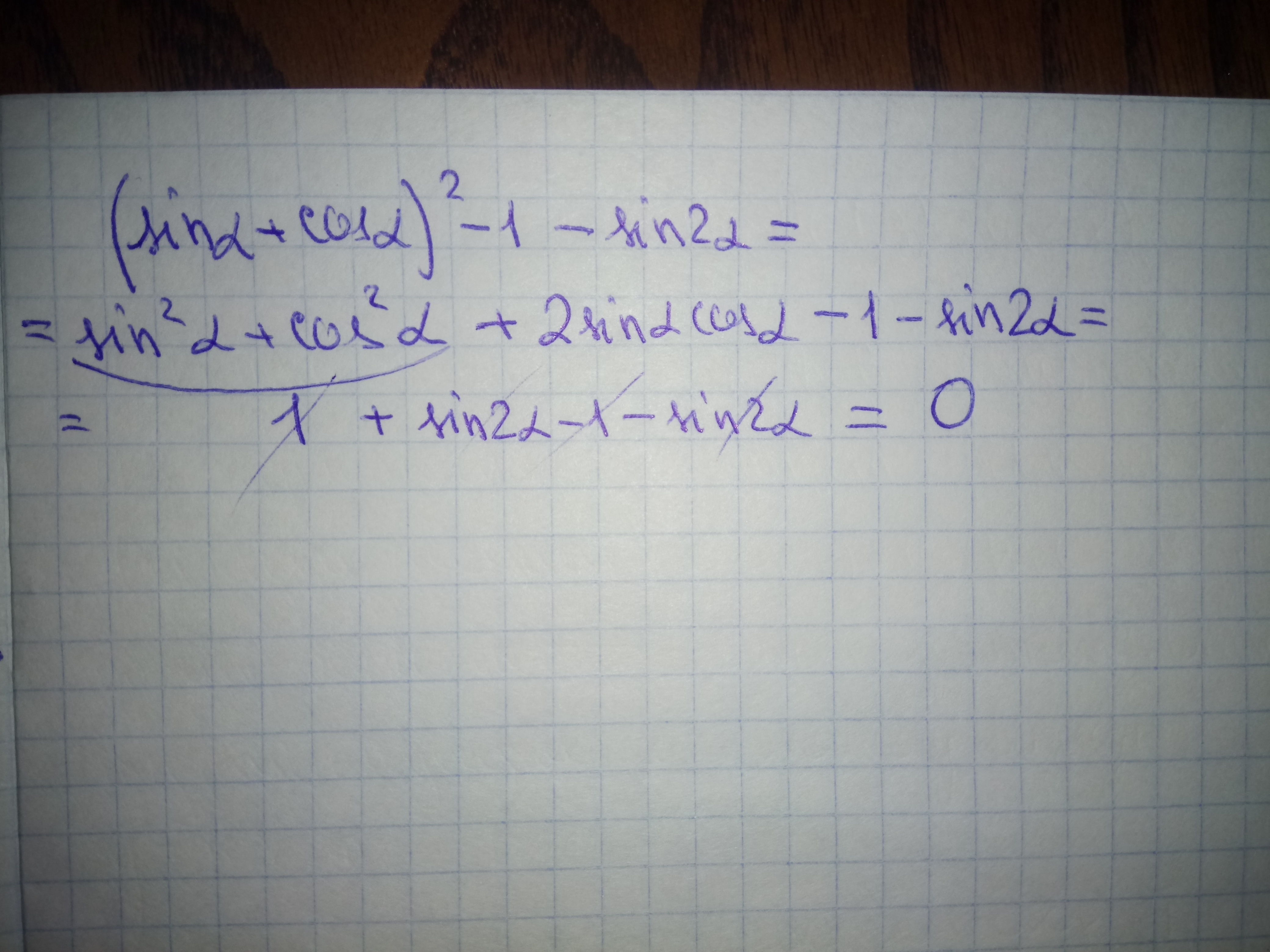
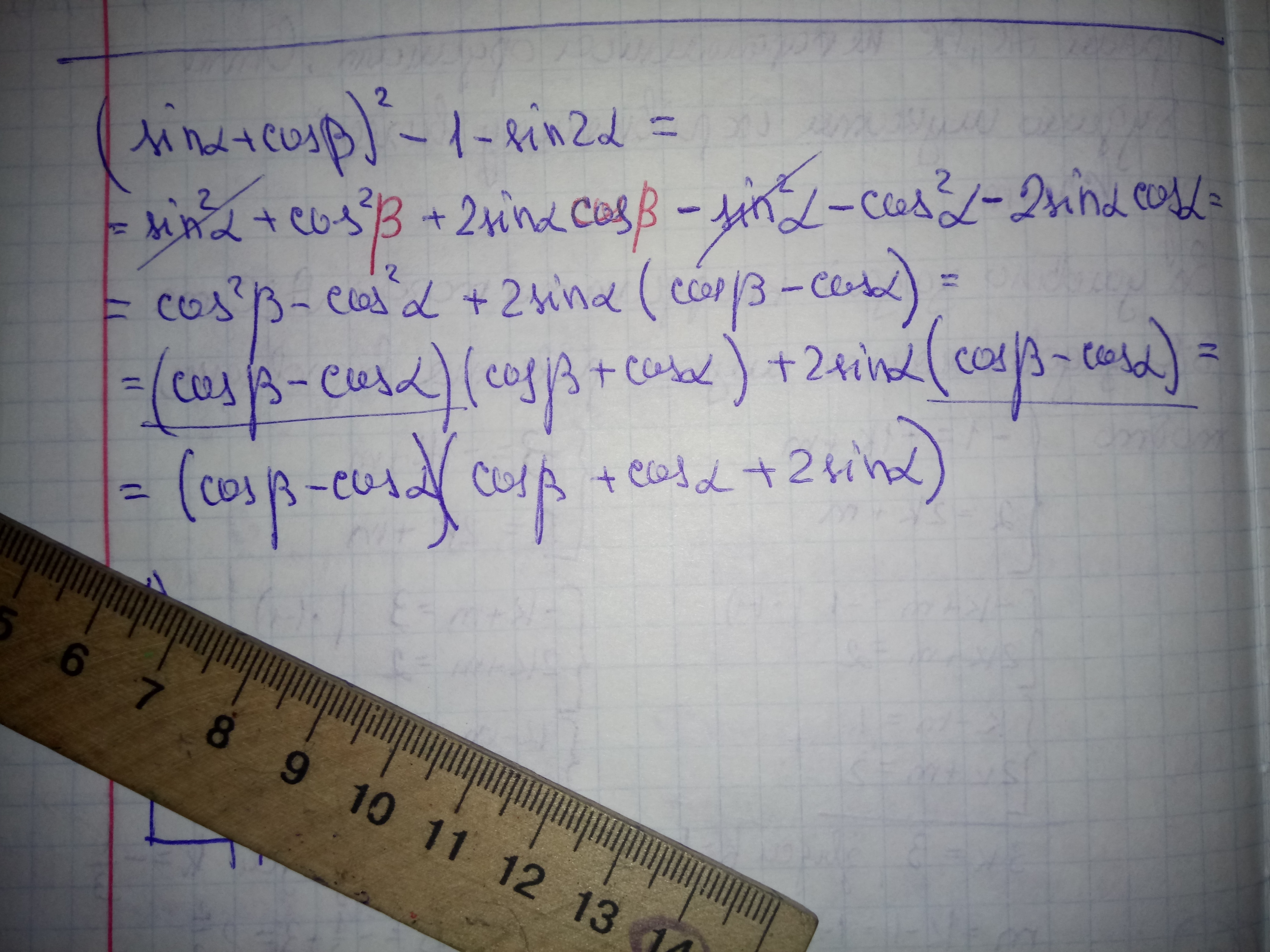
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Другие предметы,
автор: mm0400
Предмет: Английский язык,
автор: vitalikpilsikov5902
Предмет: Математика,
автор: ттайна
Предмет: История,
автор: kmrf123