Решить уравнение.

Ответы
нужно перенести все влево и разложить на множители...
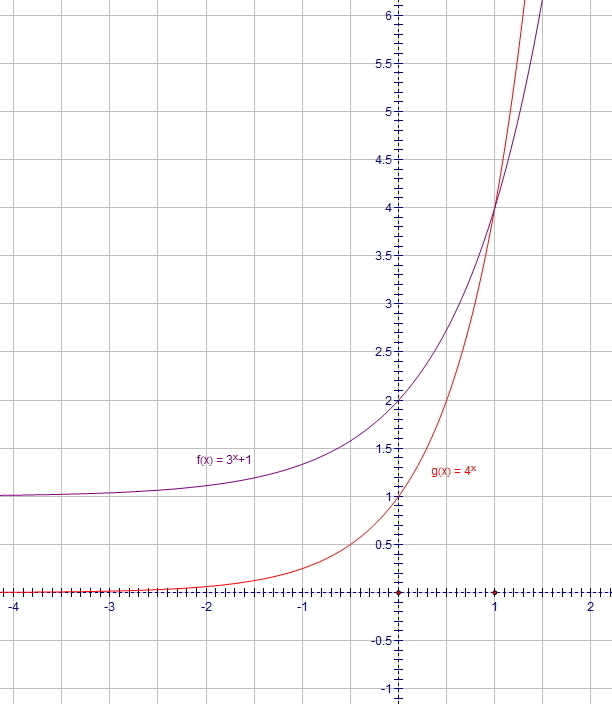
второе из получившихся уравнений решается графически: обе показательные функции монотонно возрастают, потому решение (если оно есть) будет единственным...

task/29774019 Решить уравнение. 9ˣ +4ˣ =12ˣ +1
Решение: 9ˣ + 4ˣ =12ˣ + 1. ⇔(3ˣ)² - 1 + 4ˣ -12ˣ =0. ⇔ (3ˣ -1 )(3ˣ +1 ) -4ˣ( 3ˣ - 1) = 0 . ⇔(3ˣ - 1) (3ˣ+1 - 4ˣ) =0. ⇔ [ 3ˣ -1 =0 ; 3ˣ + 1 = 4ˣ . ⇔ [ 3ˣ = 1 ; (3/4)ˣ + (1/4)ˣ = 1 . ⇔ [ 3ˣ =3⁰ ; (3/4)ˣ+(1/4)ˣ = 1 . ⇔
[ 3ˣ = 3⁰ ; (√3 / 2)²ˣ+(1/2)²ˣ = 1 . ⇔ [ x =0 ; 2x=2.
ответ : 0 ; 1.
(√3 / 2)²ˣ+(1/2)²ˣ =1 → (sinφ)²ˣ +(cosφ)²ˣ = 1 || здесь φ =60° || → 2x =2 ; x = 1.
по другому : (3/4)ˣ+(1/4)ˣ = 1 ; очевидно x=1 корень этого уравнения можно обосновать , что нет других решений . от противного
если x < 1 ⇒ (√3 / 2)²ˣ + (1/2)²ˣ > (√3 / 2)² +(1 / 2)² = 1
если x > 1 ⇒ (√3 / 2)²ˣ + (1/2)²ˣ > (√3 / 2)² +( 1/2)² = 1