Question

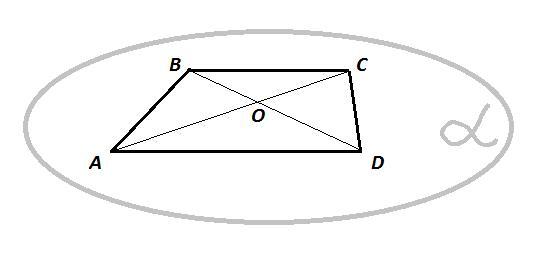
две смежные вершины и точка пересечения диагоналей трапеции лежат в плоскости а. Докажите что и остальные  две вершини лежат в плоскости (а)

Answer 1

Дано : плоскость α ;  трапеция ABCD,  BC║AD;

           A∈α , B∈α ;    AC∩BD=O;   O∈α

Доказать :   C∈α , D∈α

Доказательство :

AC - диагональ трапеции, О - точка пересечения диагоналей трапеции  ⇒   точки A, O и С  лежат на одной прямой, содержащей диагональ AC.  Так как две точки этой прямой принадлежат плоскости α по условию, то вся прямая лежит в плоскости α :

A∈AC,  A∈α,  О∈AC,  O∈α  ⇒  AC⊂α   ⇒    C∈α

BD - диагональ трапеции, О - точка пересечения диагоналей трапеции  ⇒   точки B, O и D  лежат на одной прямой, содержащей диагональ BD.  Так как две точки этой прямой принадлежат плоскости α по условию, то вся прямая лежит в плоскости α :

B∈BD,  B∈α,  О∈BD,  O∈α  ⇒  BD⊂α   ⇒    D∈α

A∈α , B∈α , C∈α , D∈α   -  все вершины трапеции в плоскости α

$blacksquare$