Предмет: Математика,
автор: cocirmariadenis
Один из корней квадратного уравнения 3х² +8х-4=0 положителен. НЕ РЕШАЯ, ОПРЕДЕЛИТЬ ЗНАК ВТОРОГО КОРНЯ.
Ответы
Автор ответа:
2
Разделив обе части уравнения на 3, получим:

По теореме виета x₁x₂ = -4/3 < 0. По условию x₁ > 0, следовательно, x₂ < 0.
По теореме виета x₁x₂ = -4/3 < 0. По условию x₁ > 0, следовательно, x₂ < 0.
Автор ответа:
0
ответ смотри на фото
Приложения:
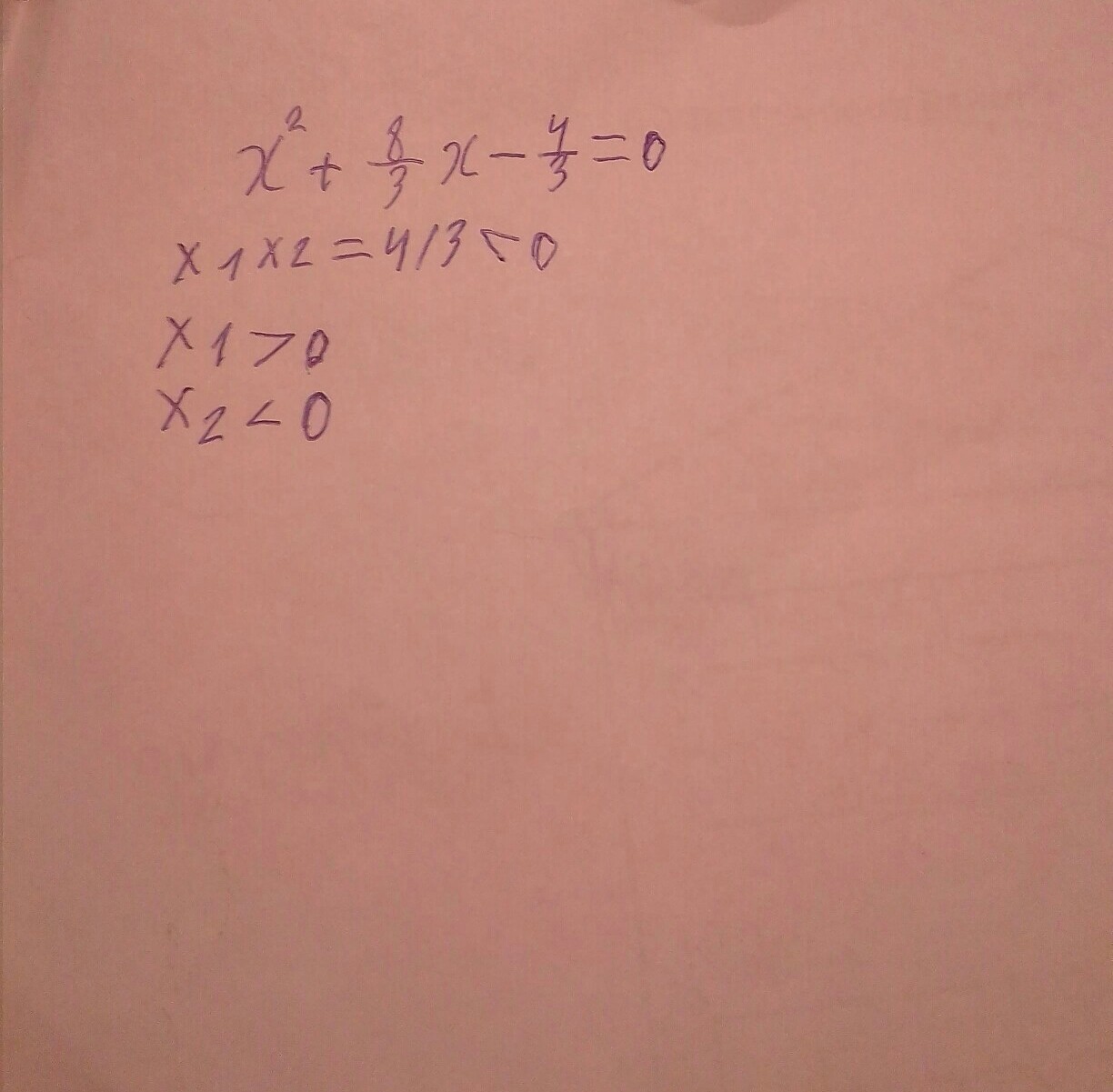
Похожие вопросы
Предмет: Математика,
автор: ppau31513
Предмет: Математика,
автор: myrzabekovalinur24
Предмет: Алгебра,
автор: LiliaNemceva
Предмет: Информатика,
автор: katakovalcuk9
Предмет: Математика,
автор: aintteyen