Предмет: Алгебра,
автор: Фиалка2332
Помогите выполнить задание, спасибо
Приложения:
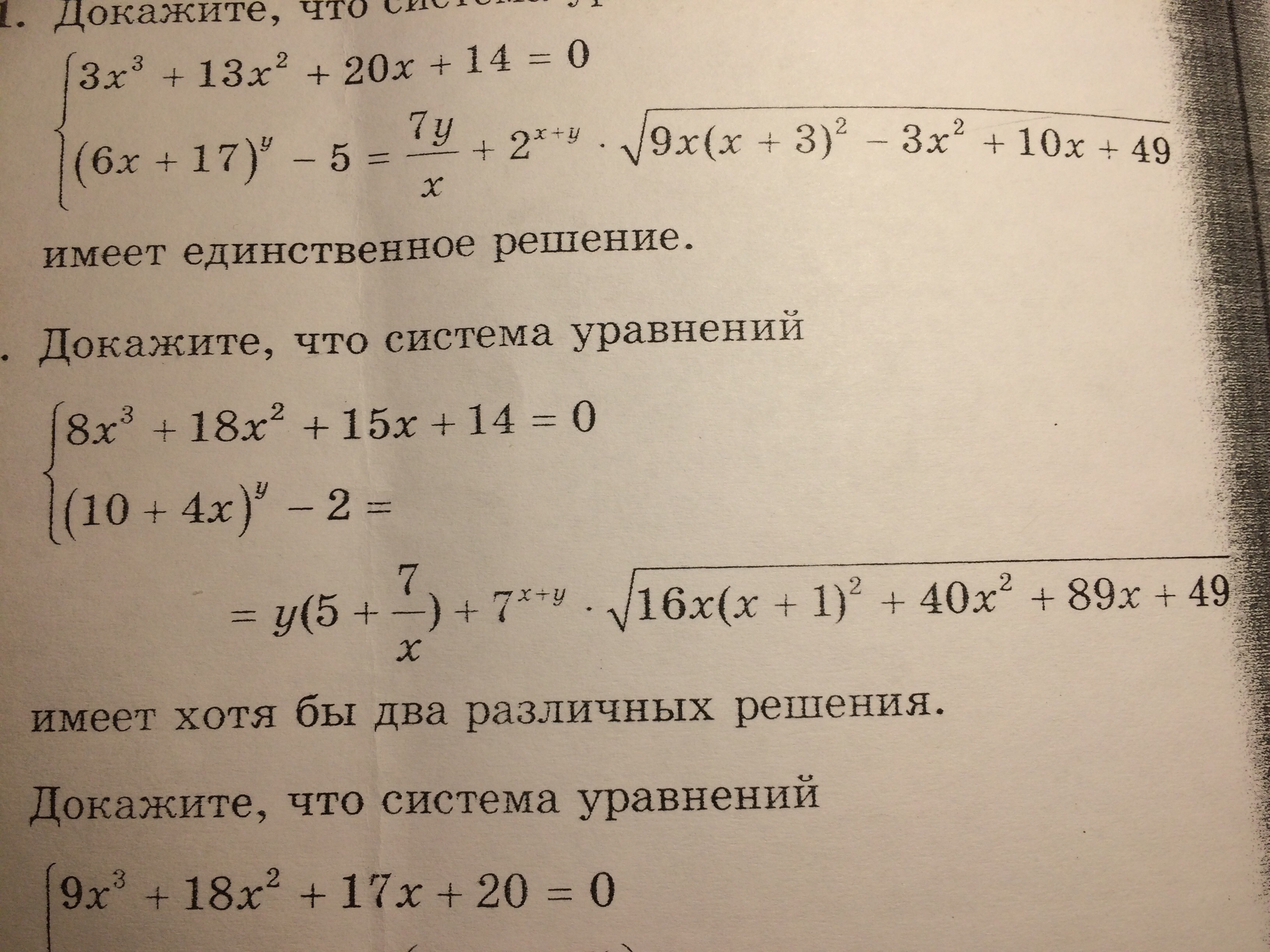
Аноним:
Про хотя бы два различных корня?
Да, именно так
Ответы
Автор ответа:
1
Первое уравнение можно решить методом разложения на множители.
Произведение равно нулю, если хотя бы один из множителей равен нулю
Здесь квадратное уравнение решений не имеет, так как D = -15 < 0.
Подставим теперь найденный корень первого уравнения во второе уравнение вместо х.
Это уравнение можно решить графически. Здесь графики пересекаются в двух точках, следовательно, система уравнений имеет хотя бы два решения.
P.S. хотя бы два решения это значит имеет два решения и больше
Приложения:
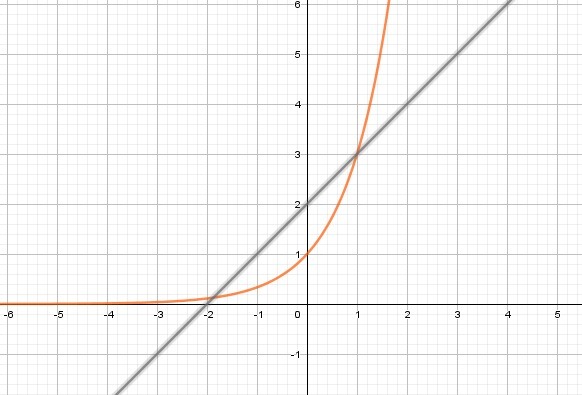
Я не совсем понимаю какими функциями заданы графики?
y+2 - прямая
3^y - показательная функция
Похожие вопросы
Предмет: Другие предметы,
автор: nimatova
Предмет: Английский язык,
автор: gfdssww
Предмет: Русский язык,
автор: Andrey666777
Предмет: География,
автор: idkdgxkdbd