Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста! Заранее благодарю!
Приложения:
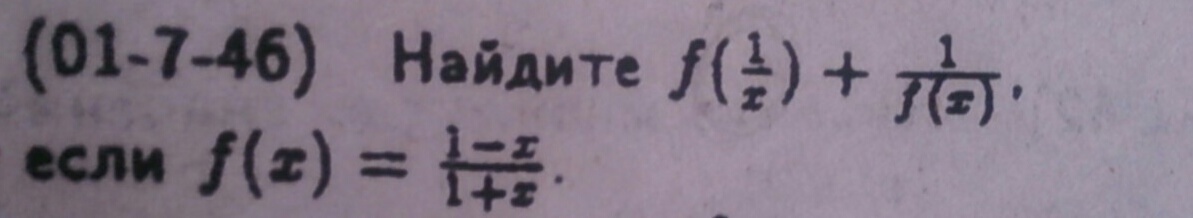
Ответы
Автор ответа:
1
Найдем теперь сумму
Аноним:
f(x) у вас уже дано нужно подставить x=1/x
Похожие вопросы
Предмет: Алгебра,
автор: Curene
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: ballezza
Предмет: Математика,
автор: Zura121313
Предмет: Математика,
автор: Аноним