Предмет: Алгебра,
автор: salve12
Найти те значения переменных, при которых заданное выражение принимает наименьшее значение. (4x-7y-33)^2+(2x+5y-25)^4-3=0
Решить системой уравнений, такой блок заданий, 6.1 - 6.4 нормально решались, методами сложения, подстановки и т.п., а тут многоуровневая система какая-то. Заранее спасибо
Приложения:
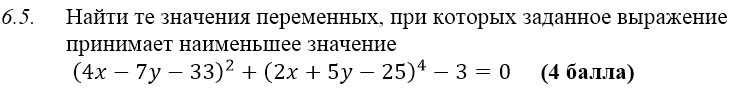
Guardian07:
Согласен с вами,нужно приравнять к нулю и решить систему
Ответы
Автор ответа:
1
Поскольку первая скобка в квадрате,а вторая в четвертой степени,то выражение положительно или равно нулю. Значит минимальное значение,которое принимает выражение и есть 0. Чтобы это произошло,нужно,чтобы две скобки одновременно равнялись нулю.
Решение во вложении. Удачи
Приложения:

все выражение равняется 0
Спасибо, но я недопонимию самый первый этап решения. У нас же есть -3, получается что 0+0-3=0? Я приравнивал 0 и к 3, но почему надо к двум нулям?
ну так напишите тогда,как это сделать
ну почему же не напишите полный развернутый ответ?
Мне кажется, мы по разному понимали слово "выражение". Для меня это (4x-7y-33)^2+(2x+5y-25)^4-3=0, для него минимальным значением при х=10 и у=1 будет -3, так как скобки в квадрате. Спасибо, теперь когда я сам это написал я понял
Похожие вопросы
Предмет: Математика,
автор: n12071978
Предмет: Биология,
автор: ashaimov43
Предмет: Английский язык,
автор: karinasvercova
Предмет: Химия,
автор: Мария7542