Предмет: Математика,
автор: vasilevaaska
Решить с развёрнутым ответом
Приложения:
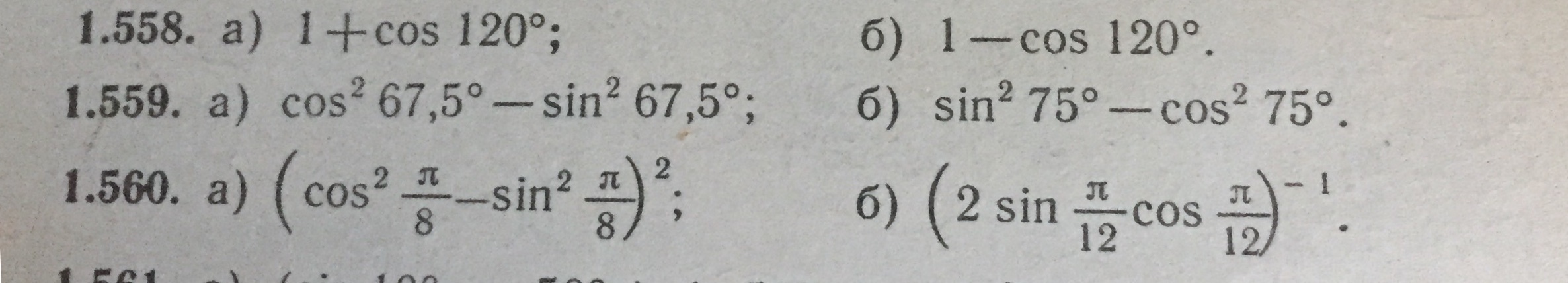
Ответы
Автор ответа:
1
1.558
а) Используем формулу понижения степени:

б)

1.559.
а) Используем формулу косинуса двойного угла:


б)

1.560
а)

б) Используем формулу синуса двойного угла


а) Используем формулу понижения степени:
б)
1.559.
а) Используем формулу косинуса двойного угла:
б)
1.560
а)
б) Используем формулу синуса двойного угла
Похожие вопросы
Предмет: Математика,
автор: arystanergazinov
Предмет: Математика,
автор: nastyuha2uha
Предмет: Литература,
автор: Аноним
Предмет: Информатика,
автор: tweterte
Предмет: География,
автор: elenaknyazeva3