Предмет: Алгебра,
автор: kirill55413
Помогите, с помощью графиков выясните, какая система не имеет решиний, а какая имеет бесконечно много решений, в последнем случае укажите какое нибудь решение системы
Приложения:
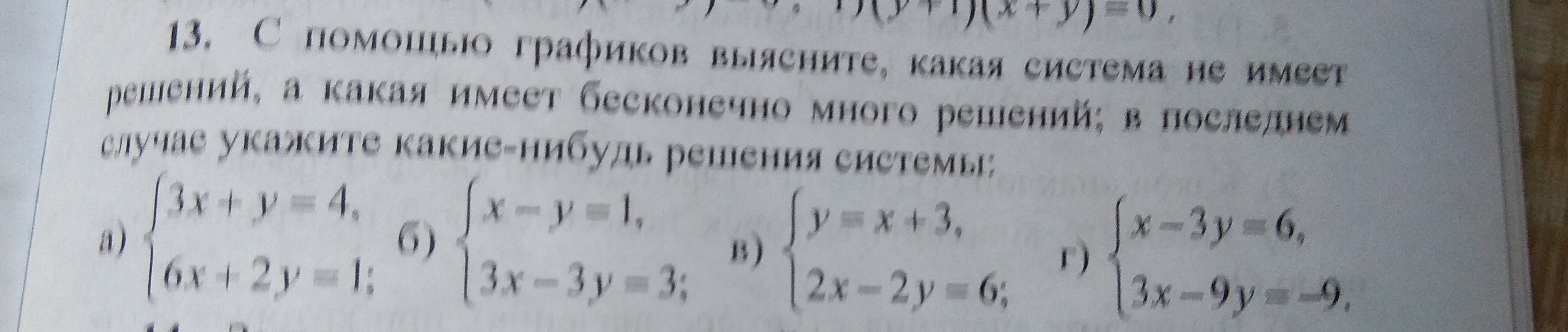
Ответы
Автор ответа:
2
Уравнение прямой имеет вид:
Пусть дана система из 2-х уравнений:
Если коэффициенты не пропорциональны, то прямые не параллельны, а пересекаются (следует из векторных соображений)
Если коэффициенты пропорциональны, то прямые параллельны, здесь нужно понимать особый случай - совпадение
1) - пересечение
2) - параллельность
3) - совпадение
1 - 1 решение
2 - нет решений
3 - бесконечное кол-во решений
а) - нет решений
б) - бесконечное множество
в) - нет решений
г) - нет решений
Похожие вопросы
Предмет: Алгебра,
автор: Thatgirl
Предмет: Геометрия,
автор: luganskaavika334
Предмет: Математика,
автор: polinkee
Предмет: Математика,
автор: loloalenka
Предмет: Алгебра,
автор: knockoutmna