Помогите пожалуйста с заданием 5(6)

Ответы
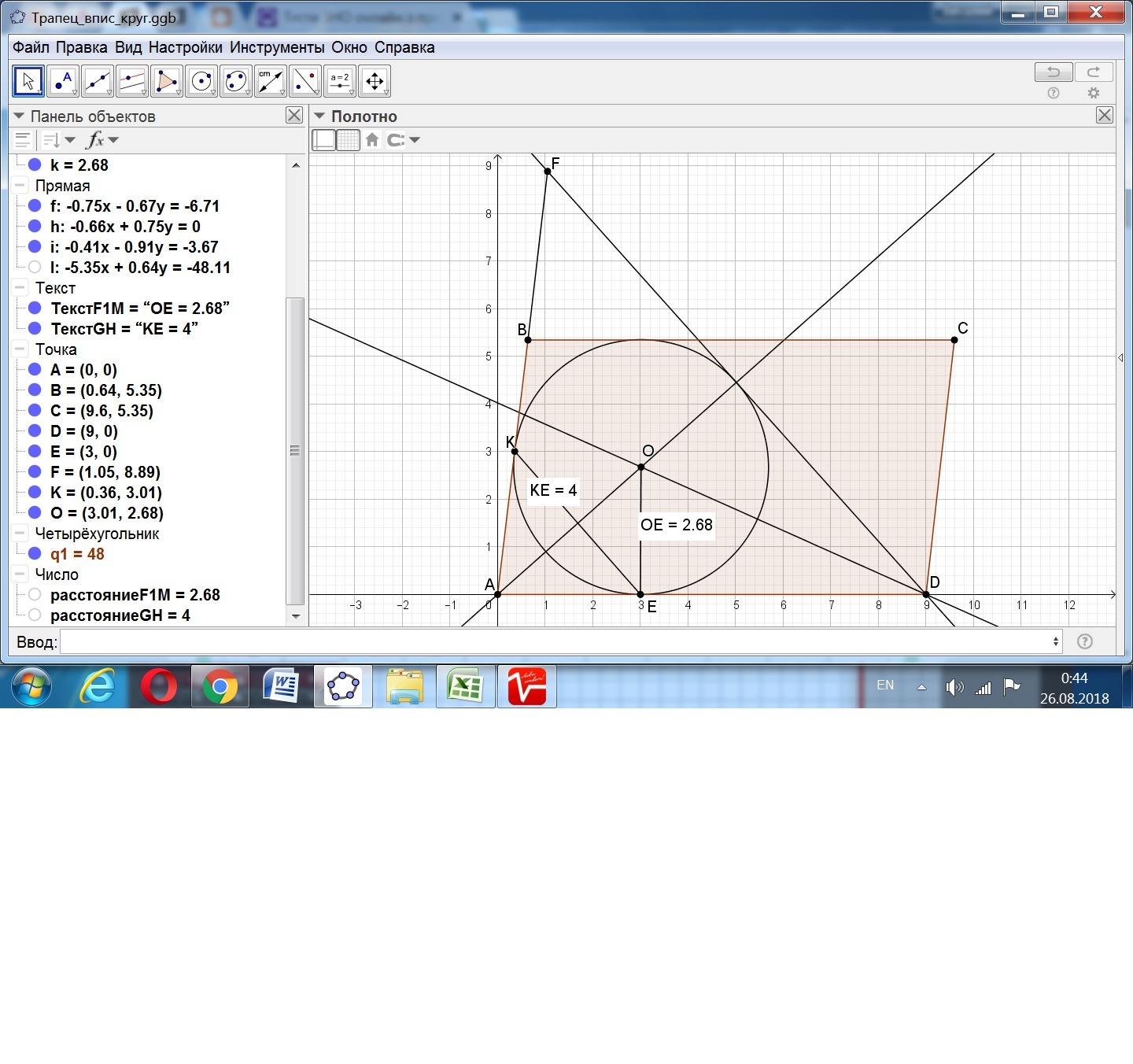
а) Пусть точка О - центр окружности с радиусом R.
Пересечение биссектрис - точка М.
Обозначим АЕ = х, МД = 9 - х.
Биссектрисы параллелограмма пересекаются под прямым углом.
Хорда КЕ перпендикулярна биссектрисе АМ.
Половина хорды КЕ = 2. Из подобия треугольников составим пропорцию:
2/х = (9 - х) / 9.
18 = 9х - х². Получили квадратное уравнение х² - 9х + 18 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-9)^2-4*1*18=81-4*18=81-72=9;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(2root9-(-9))/(2*1)=(3-(-9))/2=(3+9)/2=12/2=6;
x_2=(-2root9-(-9))/(2*1)=(-3-(-9))/2=(-3+9)/2=6/2=3.
Так как АЕ < ЕД, то принимаем меньшее значение х = АЕ = 3.
Из прямоугольного треугольника АОЕ имеем уравнение:
х*R = 2*AO.
AO = √(x² + R²) = √(9 + R²). Подставим: 3*R = 2*√(9 + R²).
Возведём в квадрат: 9R² = 4(9 + R²) = 36 + 4R².
5R² = 36, отсюда R = 6/√5 = 6√5/5 ≈ 2,683281573 см.
б) Площадь параллелограмма равна 2R*9 = 12√5/5 ≈ 48,29906831 см².