Предмет: Алгебра,
автор: kisonix
Найти сумму корней уравнения
Приложения:
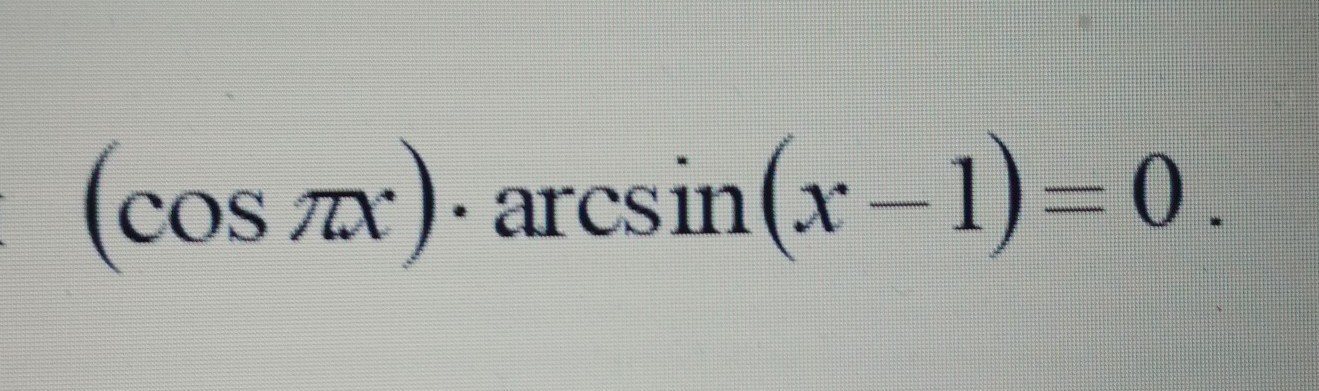
Ответы
Автор ответа:
2
ОДЗ уравнения
-1≤х-1≤1
0≤х≤2
уравнение распадается на следующие:
cos πх=0 и arcsin(x-1)=0
cos πх=0
πх=½π+πn, n€Z
x=½+n, n€Z
вернёмся к ОДЗ
0≤½+n≤2
т.к n€Z, то n=0, n=1
при n=0 x1=½
при n=1 x2=1½
arcsin(x-1)=0
x-1=0
x3=1
Следовательно,суммa корней уравнения:
x1+x2+x3=½+1½+1=3
Ответ: 3
Удачи!
mishka19:
нет ОДЗ, ведь у арксинус определен не на всей числовой прямой
напишите сюда одз
Автор ответа:
3
ОДЗ

.......................
cos πx=0 или arcsin(x-1)=0
Первое уравнение:

найдем корни с учётом ОДЗ

так как n-целое число, то

если

, то

если

, то

Второе уравнение

Сумма корней уравнения

Ответ: 3
.......................
cos πx=0 или arcsin(x-1)=0
Первое уравнение:
найдем корни с учётом ОДЗ
так как n-целое число, то
если
, то
если
, то
Второе уравнение
Сумма корней уравнения
Ответ: 3
Похожие вопросы
Предмет: Геометрия,
автор: tanya0727
Предмет: Химия,
автор: steph012
Предмет: Українська мова,
автор: Vechenveched
Предмет: Биология,
автор: blacksheep455
Предмет: Математика,
автор: AlinaKraynik