Предмет: Геометрия,
автор: Lanosha
На окружности отмечены точки A и B так, что меньшая дуга AB равна 168°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах
Приложения:
Ответы
Автор ответа:
113
Ответ: 84°
Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Объяснение:
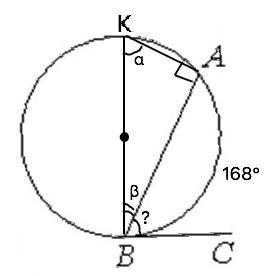
Проведем диаметр ВК и соединим К и А. Треугольник ВАК прямоугольный ( угол КАВ опирается на диаметр). Сумма острых углов прямоугольного треугольника 90° =>
∠АКВ+∠КВА= 90°
Диаметр, проведенный в точку касания перпендикулярен касательной.
∠КВС°= ∠КВА+АВС=90°. Но и ∠ АКВ+∠КВА=90°. В сумме 90° имеется по равному слагаемому, следовательно, вторые слагаемые тоже равны. ⇒
УголАВС равен вписанному углу АКВ.
Вписанный угол равен половине градусной меры дуги, на которую опирается
∠АВС=∠АКВ=168°:2=84°
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: miamil
Предмет: Математика,
автор: lizabrackova02
Предмет: Математика,
автор: malikazhapar11
Предмет: Информатика,
автор: championZSP
Предмет: Математика,
автор: KisaAnya