Предмет: Алгебра,
автор: Voskabueva
Распишите решение ПОДРОБНО
спасибо большое
Номера 1. 2 и 7
Приложения:
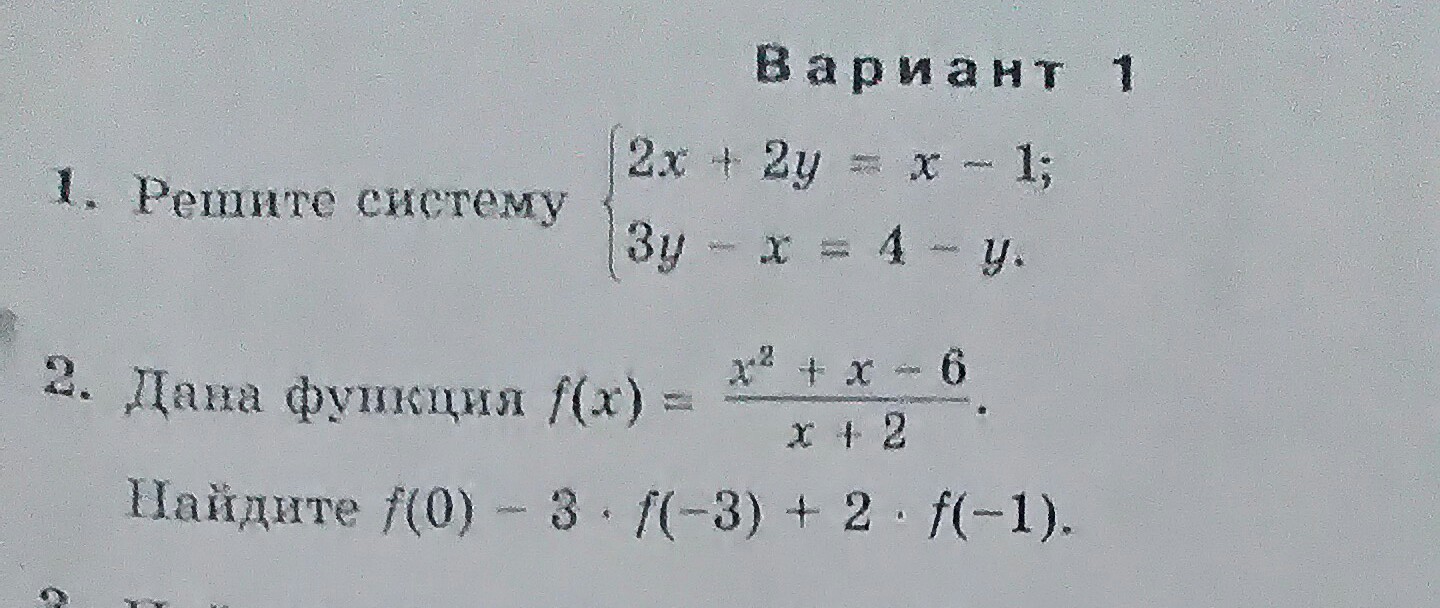
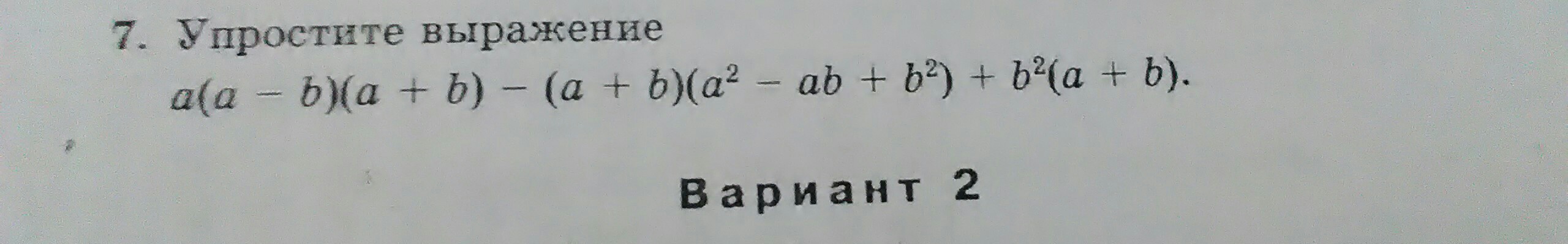
Planar:
Номер 1 получился в комментариях под ответом
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Химия,
автор: Thisnameistaken
Предмет: Русский язык,
автор: as5088054
Предмет: Математика,
автор: aliserzakupov49
Предмет: Алгебра,
автор: gooogleoa
Предмет: Математика,
автор: EgorFed1