Предмет: Алгебра,
автор: Masha122333
Помогите решить неравенство
Приложения:
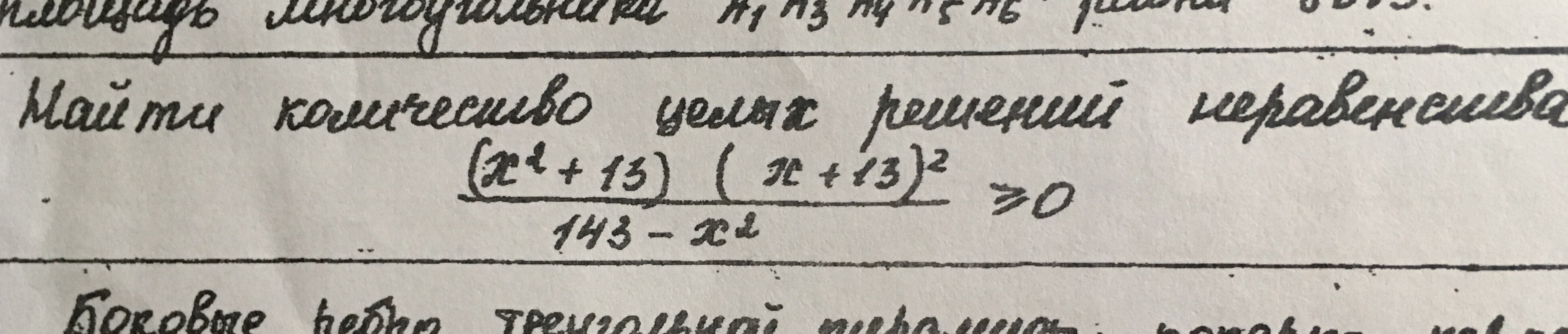
sherlok123321:
ответ есть?
Ответы
Автор ответа:
0
так как x²+13≥13 и (x+13)²≥0 при любых x, то неравенство можно представить в виде следующей совокупности:
11=√121<√143<√144<12 ⇒ -11>-√143>-12
Ответ: 24
сами целые решения: -13, -11, -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Похожие вопросы
Предмет: Математика,
автор: maksimtop20092
Предмет: История,
автор: sofa7468gmailcom
Предмет: Английский язык,
автор: zauharsanatova
Предмет: Математика,
автор: милана20062
Предмет: Математика,
автор: али177