Предмет: Алгебра, автор: ternovka1721

Найдите все значения параметра а такие, что f(x) является непрерывной на всей числовой прямой, если

Приложения:

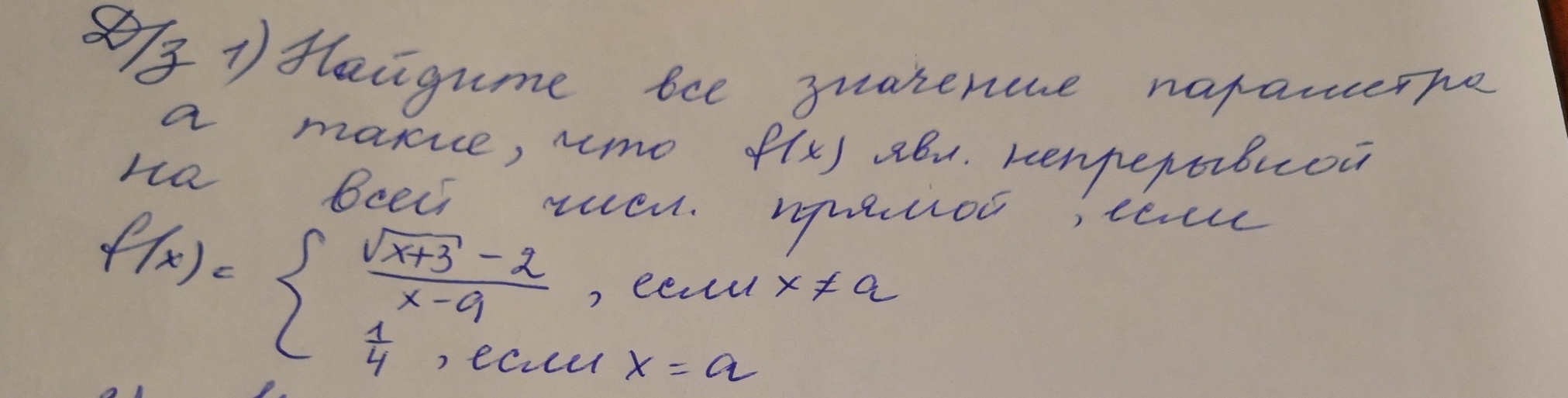
Аноним: Условие некорректное, так как из-за корня, функция определена только при x>=-3

Аноним: а графиком f(x) = 1/4, при x=a, является точка! Если б f(x) = 1/4, при x>a или наоборот <0, то можно было бы решать

Аноним: Или можно дать ответ, что нет таких значений "а"

Ответы

Автор ответа: qwaaq

условие непрерывности данной функции можно записать как

$f(a)= \lim_{x \to a} \frac{\sqrt{x+3} -2}{x-a} =\frac{1}{4}$

Рассмотрим то что под знаком предела. При любых a (и, следовательно, иксах стремящихся к а) кроме единицы предела, строго говоря, существовать не будет, мы получим соотношение вида константа делить на ноль, т.е. бесконечно большую величину.

При единице будет неопределенность вида $\frac{0}{0}$ , тут уже величина предела может оказаться конечной. Раскрыв неопределенность (например по пр. Лопиталя ) получим число 1/4; т.е. функция будет непрерывна.