Предмет: Алгебра,
автор: sizuz
Найдите кол-во целых чисел из области определения функции
Приложения:
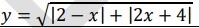
Ответы
Автор ответа:
1
D(y):
|2 - x| + |2x + 4| ≥ 0 (*).
Так как |2 - x| ≥ 0 и |2x + 4| ≥ 0, то |2 - x| + |2x + 4| ≥ 0. Следовательно, выражение (*) справедливо для всех x ∈ R. Это означает, что в область определения функции y входит все множество целых чисел.
MusikaWinx:
Ответ: Z (множество всех целых чисел). Количество таких чисел бесконечно.
Автор ответа:
1
Количество целых чисел из области определения бесчисленно много.
А ответ какой? Нет ответа? Или 0
У меня вот по другому получилось
Похожие вопросы
Предмет: Алгебра,
автор: vikotrya
Предмет: Информатика,
автор: sweeg66
Предмет: Математика,
автор: gufmarina3986
Предмет: Математика,
автор: мустанг4
Предмет: Алгебра,
автор: gospodi1