Предмет: Математика,
автор: ctrelo4nik17
помогите решить пределы пожалуйста!
Приложения:
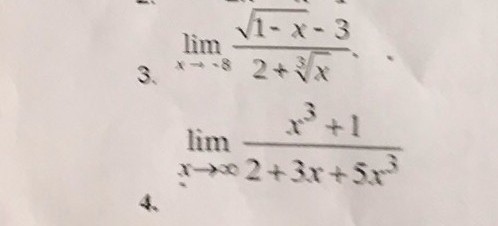
Ответы
Автор ответа:
0
3)
![lim \frac{ \sqrt{1 - x} - 3 }{2 + \sqrt[3]{x} } = ( \frac{0}{0} ) = lim\frac{ \frac{ -1}{2 \sqrt{1 - x} } }{ \frac{1}{3} \times {x}^{ - \frac{2}{3 } } } = lim \frac{ - 3 {x}^{ \frac{2}{3} } }{2 \sqrt{1 - x} } = \frac{ - 3 \times \sqrt[3]{64} }{2 \sqrt{9} } = \frac{ - 3 \times 4}{2 \times 3} = - 2 lim \frac{ \sqrt{1 - x} - 3 }{2 + \sqrt[3]{x} } = ( \frac{0}{0} ) = lim\frac{ \frac{ -1}{2 \sqrt{1 - x} } }{ \frac{1}{3} \times {x}^{ - \frac{2}{3 } } } = lim \frac{ - 3 {x}^{ \frac{2}{3} } }{2 \sqrt{1 - x} } = \frac{ - 3 \times \sqrt[3]{64} }{2 \sqrt{9} } = \frac{ - 3 \times 4}{2 \times 3} = - 2](https://tex.z-dn.net/?f=lim+%5Cfrac%7B+%5Csqrt%7B1+-+x%7D+-+3+%7D%7B2+%2B++%5Csqrt%5B3%5D%7Bx%7D+%7D++%3D+%28+%5Cfrac%7B0%7D%7B0%7D+%29+%3D++lim%5Cfrac%7B+%5Cfrac%7B+-1%7D%7B2+%5Csqrt%7B1+-+x%7D+%7D+%7D%7B+%5Cfrac%7B1%7D%7B3%7D+%5Ctimes++%7Bx%7D%5E%7B+-++%5Cfrac%7B2%7D%7B3+%7D+%7D++%7D++%3D+lim+%5Cfrac%7B+-+3+%7Bx%7D%5E%7B+%5Cfrac%7B2%7D%7B3%7D+%7D+%7D%7B2+%5Csqrt%7B1+-+x%7D+%7D++%3D++%5Cfrac%7B+-+3+%5Ctimes++%5Csqrt%5B3%5D%7B64%7D+%7D%7B2+%5Csqrt%7B9%7D+%7D++%3D++%5Cfrac%7B+-+3+%5Ctimes+4%7D%7B2+%5Ctimes+3%7D++%3D++-+2)
4)

4)
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: LenaTuraev
Предмет: Литература,
автор: samikaa89
Предмет: Литература,
автор: jenechka13
Предмет: Литература,
автор: savi2781
Предмет: Математика,
автор: МилкиВэй2005