Question

Сколько решений имеет уравнение log₃(x+2) = 2 - |x| ?

Answer 1

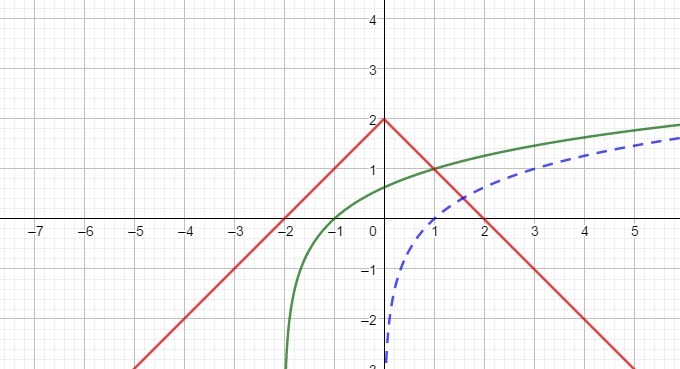
log₃(x+2) = 2 - |x|.

Задачу решаем графически.

Рассмотрим функции у = log₃(x+2) и у = 2 - |x| и построим их графики.

1) у = log₃(x+2). Воспользуемся методом геометрических преобразований.

1. Строим график функции у = log₃(x) при x > 0;

2. Выполним параллельный перенос графика функции у = log₃(x) на 2 единицы влево и получим график функции у = log₃(x+2).

2) у = 2 - |x|. Также построим при помощи метода геометрических преобразований.

1. Строим график функции у = 2 - x при x ≥ 0;

2. Отобразим график функции у = 2 - x при x ≥ 0 симетрично относительно оси ординат и получим график функции у = 2 - |x|. Графики во вложении. Ка видно из построения, данное уравнение имеет только одно решение.