Предмет: Математика,
автор: ASDvxcopk
Решите с объяснением уравнение
6^x + 9^x = 2^2x+1
Ответы
Автор ответа:
1
Ответ: 0.
Приложения:
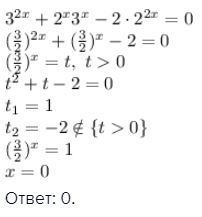
Burzumistr:
А не могли бы объяснить откуда взялось в первой строчке -2*2^(2x) ???
Так он просто перенёс и представил степень 2x+1 как произведение ,то есть воспользовался свойством степеней 7 класса
Понятно) надо скобки ставить!
А я голову ломал как от 1 избавиться, а она оказывается относится к степени...
Автор ответа:
1
Больше точек мы не будем брать ,так как мы понимаем как будет выглядеть график и строить его нет смысла
Я взял третью точку ,чтобы было понятно ,чем отличается (построением) первый график и второй .Мы видим ,что есть пересечение (x;y)=(0;2)
Ответ: 0
Похожие вопросы
Предмет: История,
автор: sasarodnikova
Предмет: Биология,
автор: evaanzorova0
Предмет: Английский язык,
автор: gofuhvjo
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: samoylenkoelka