Предмет: Алгебра,
автор: marinosnbp5jakj
решить неравенство logx-6|x-10|<=1
Ответы
Автор ответа:
1
Метод рационализации.
Приложения:

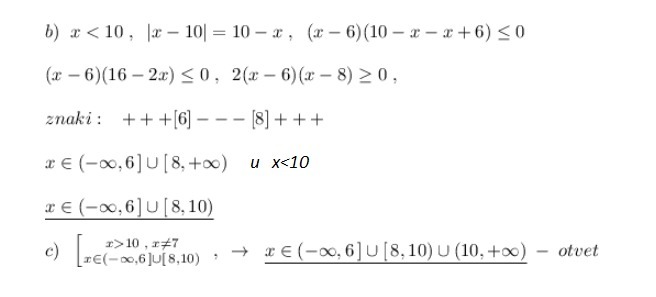
marinosnbp5jakj:
Не понятно
перезагрузи страницу, формулы отобразятся (не с телефона)
Спасибо
Похожие вопросы
Предмет: Алгебра,
автор: kolapulaho
Предмет: Математика,
автор: vladazhh
Предмет: Алгебра,
автор: Chuchulu
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: Аноним