Предмет: Математика,
автор: Аноним
срочно срочно срочно срочно
Приложения:
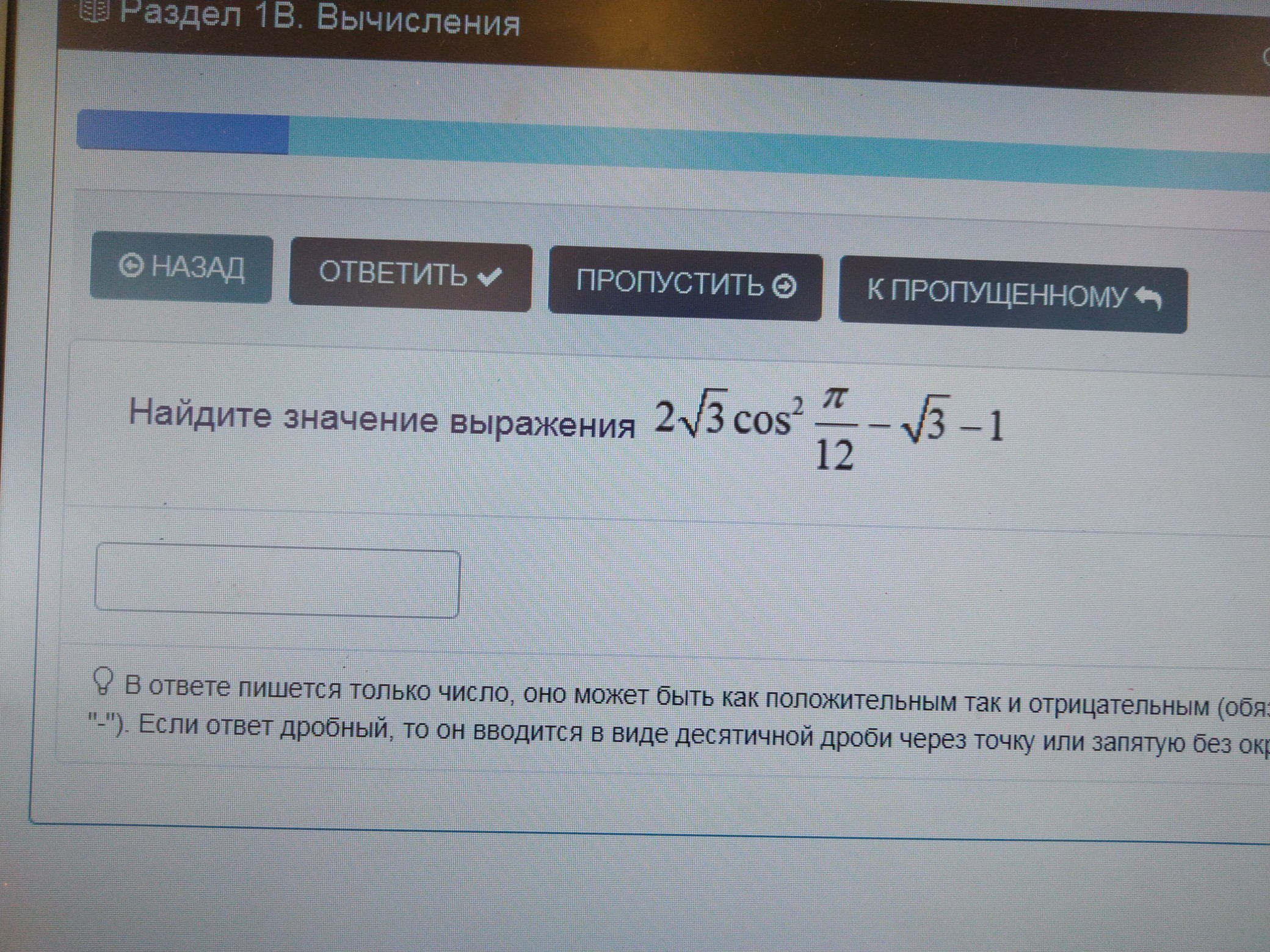
Ответы
Автор ответа:
2
Применил формулу:
ОТВЕТ: 0,5
Автор ответа:
1
Используя формулу cos(,записать выражение в развёрнутом виде:
;
Вычислить выражение,используя таблицу значений тригонометрических функций:
;
Сократить числа на 2:
;
Распределить через скобки:
;
Сократить противоположные выражения:
;
Вычислить разность:
Похожие вопросы
Предмет: Українська мова,
автор: vikafenko304
Предмет: География,
автор: kolb4cka228
Предмет: Алгебра,
автор: abdikarimovakmaral06
Предмет: Химия,
автор: maxim432234