Предмет: Алгебра,
автор: Vishenka3389
Алгебра. 8 класс.Помогите решить пожалуйста.Это очень срочноо!!! Буду очень благодарна.
Задание во вложении.
Приложения:
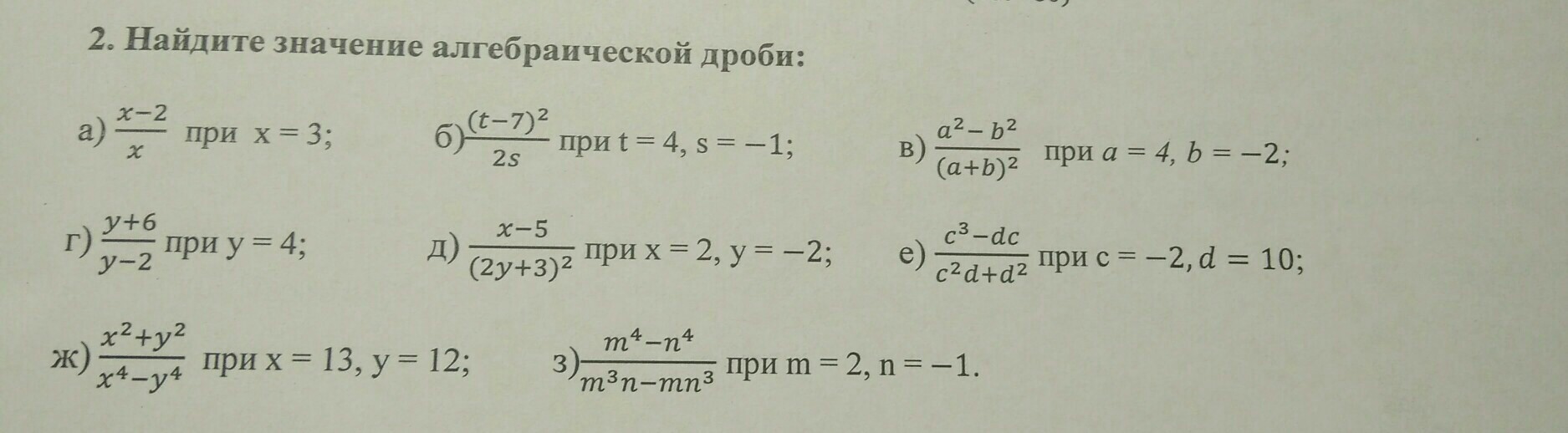
Ответы
Автор ответа:
1
а)

б)

в)

г)

д)

е)

ж)

з)

б)
в)
г)
д)
е)
ж)
з)
Vishenka3389:
Спасибо огромное ❤
Похожие вопросы
Предмет: Русский язык,
автор: eivan27011009
Предмет: Қазақ тiлi,
автор: nuraiutesheva
Предмет: Английский язык,
автор: 89370386151v
Предмет: Математика,
автор: MarSahakyan
Предмет: Химия,
автор: sergey5555444