Предмет: Геометрия,
автор: mishutka147
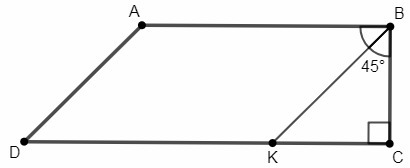
РЕБЯТ, СРОЧНО. в прямоугольной трапеции ABCD (угол C = 90°) AB : AD = 3:2. Точка K лежит на большем основании CD, AB = DK, угол CBK = углу ABK. Вычеслите длины оснований трапеции ABCD, если площадь четырехугольника ABKD равна 12 корней из 2.
Ответы
Автор ответа:
2
∠B=90° (ABCD - прямоугольная трапеция, BC⊥AB)
∠ABK=∠CBK (по условию) => ∠CBK=∠B/2 =45°
△BCK - равнобедренный (прямоугольный с углом 45°)
BC=CK
BC=√2/2 BK (в треугольнике с углами 45°, 90° стороны относятся как 1:1:√2)
ABKD - параллелограмм (противоположные стороны AB и DK равны и параллельны)
BK=AD
AD=2/3 AB (по условию)
BC=√2/3 AB
BC*AB =12√2 <=> √2/3 AB^2 =12√2 <=> AB=√(12*3)=6
CD =DK+CK =AB+BC =(1+√2/3)AB =6+2√2
Приложения:
Автор ответа:
0
6 и 6 + 2 корня из 2.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: anastasiamelehova411
Предмет: Английский язык,
автор: varuizontik554
Предмет: Английский язык,
автор: islam232353
Предмет: Химия,
автор: София252525
Предмет: Геометрия,
автор: DarkAuron34rus