Решить уравнение .Оно ниже
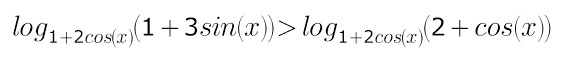
Ответы
Решить неравенство :
ОДЗ основания логарифма
ОДЗ подлогарифмических выражений
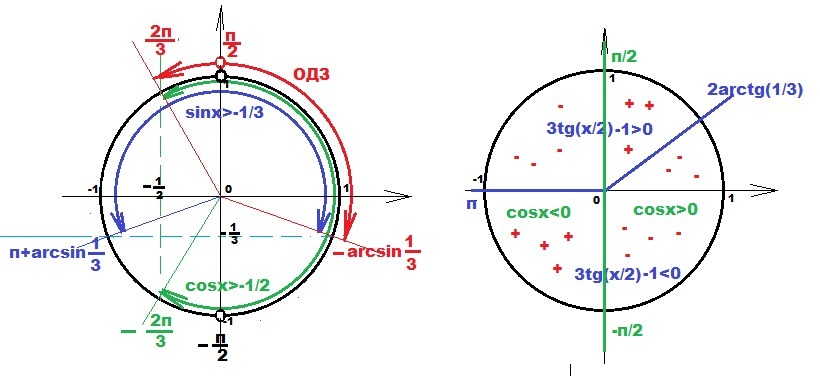
ОДЗ: x ∈ (-arcsin(1/3)+2πk; π/2+2πk)∪(π/2+2πk; 2π/3+2πk); k∈Z
Так как основания логарифмов содержат переменную х, то решение неравенства разбивается на 2 случая: основание больше единицы и основание положительное меньше единицы.
1)
Для второго неравенства системы можно воспользоваться формулами универсальной тригонометрической подстановки, так как по ОДЗ
x ≠ π + 2πk
b) 3sinx - cosx - 1 > 0
Так как знаменатель дроби 1+tg²(x/2)≥1, то знак неравенства зависит только от числителя
6 tg (x/2) - 2 > 0
tg (x/2) > 1/3
arctg (1/3) + πm < x/2 < π/2 + πm, m ∈ Z
2arctg (1/3) + 2πm < x < π + 2πm
С учетом первого неравенства и ОДЗ
x ∈ (2arctg (1/3) + 2πk; π/2 + 2πk), k ∈ Z
2)
a) -0,5 < cosx < 0. Решение состоит из двух интервалов
x ∈ (-2π/3 + 2πk; -π/2+2πk) - не подходит под ОДЗ
x ∈ (π/2 + 2πk; 2π/3 + 2πk)
b) Второе неравенство решается аналогично первой системе с помощью универсальной тригонометрической подстановки, только со знаком '<'
6 tg (x/2) - 2 < 0
tg (x/2) < 1/3
-π/2 + πp < x/2 < arctg (1/3) + πp, p∈Z
-π + 2πp < x < 2 arctg (1/3) + 2πp
Так как из первого неравенства x ∈ (π/2 + 2πk; 2π/3 + 2πk) , то данная система не имеет решений.
Ответ: x ∈ (2 arctg(1/3) + 2πk; π/2+2πk); k∈Z
==========================================
2 способ. Покороче.
ОДЗ: x ∈ (-arcsin(1/3)+2πk; π/2+2πk)∪(π/2+2πk; 2π/3+2πk); k∈Z
Метод рационализации.Неравенство
при всех допустимых значениях х равносильно неравенству
Для sinx и cosx в скобках использованы формулы универсальной тригонометрической подстановки через tg(x/2). Такая замена возможна, так как x = π + 2πh, h∈Z, в ОДЗ не входят. (п.1)
Знаки неравенства для интервала (-π; +π) с периодом 2πk
...... (-π) ++++++ (-π/2) ------- (2arctg(1/3)) ++++++ (π/2) ------ (π).......>x
С учетом периода и ОДЗ: x ∈ (2 arctg(1/3) + 2πk; π/2+2πk); k∈Z
2) 0 < 1+2cosx < 1