Предмет: Математика,
автор: Зофа25
3^(2x^2-6x+3) +6^(x^2-3x+1) =2^(2x^2-6x+3) кто нибудь объясните
Ответы
Автор ответа:
1
1) т.к. в уравнении присутствуют два разных основания (это 2 и 3), то
метод решения: делить на любое из этих оснований в старшей степени...
например, на 2^(2x^2-6x+3)...
т.е. цель: свести все к одному основанию (или (3/2) или (2/3))
...но у второго слагаемого в показателе степени останутся отличия:
6^(x^2-3x+1) : 2^(2x^2-6x+3) = 3^(x^2-3x+1) * 2^(x^2-3x+1-2x^2+6x-3) =
= 3^(x^2-3x+1) * 2^(-(x^2-3x+2))
потому я начала со свободных членов...
Приложения:
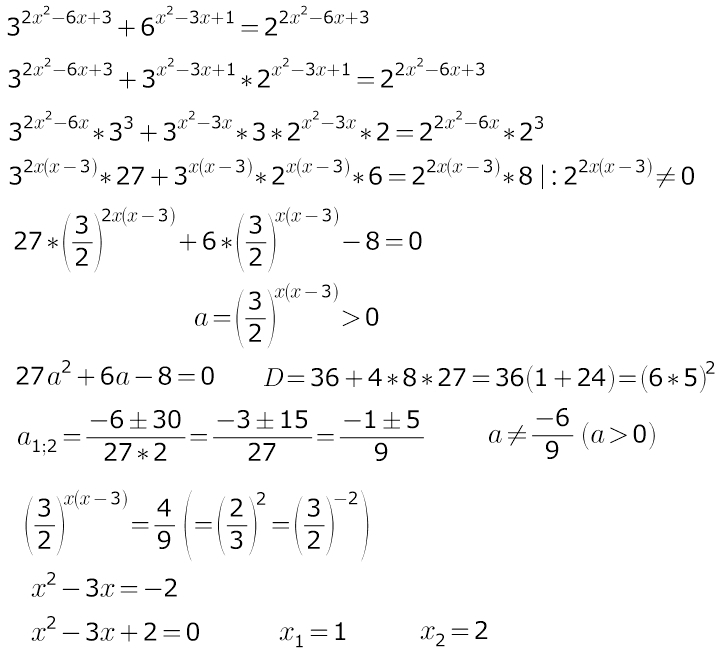
Зофа25:
Я не могу понять откуда появились после деления 3/2)^х(х-3) если сокращаем
три в степени в числителе было и осталось... а 2^ ( х(х-3) - 2х(х-3) ) = 2^ (x*x - 3x - 2x*x + 6x) = 2^ (-x*x + 3x) = 2^ ( -(x(x-3) ) получается с отрицательным показателем степени, т.е. в знаменателе...
Похожие вопросы
Предмет: Қазақ тiлi,
автор: belpd3174
Предмет: Геометрия,
автор: kekelkaner5
Предмет: Русский язык,
автор: dddllpopp
Предмет: Физика,
автор: userA