Предмет: Математика,
автор: mmilenko61
Определите промежутки возрастания и убывания функции f(x) =x^3-2x
Помогите пожалуйста.
Ответы
Автор ответа:
1
Решение задания приложено
Приложения:

Автор ответа:
1
при f'(x)>0 функция возрастает
f'(x)=3x²-2>0
f'(x)=0

возьмём точки из интервалов монотонности
см фото
f'(-1)=1 функция возрастает
f'(0)=-2 функция убывает
f'(1) =1 функция возрастает
Следовательно , при

функция убывает, при остальных х возрастает
f'(x)=3x²-2>0
f'(x)=0
возьмём точки из интервалов монотонности
см фото
f'(-1)=1 функция возрастает
f'(0)=-2 функция убывает
f'(1) =1 функция возрастает
Следовательно , при
функция убывает, при остальных х возрастает
Приложения:
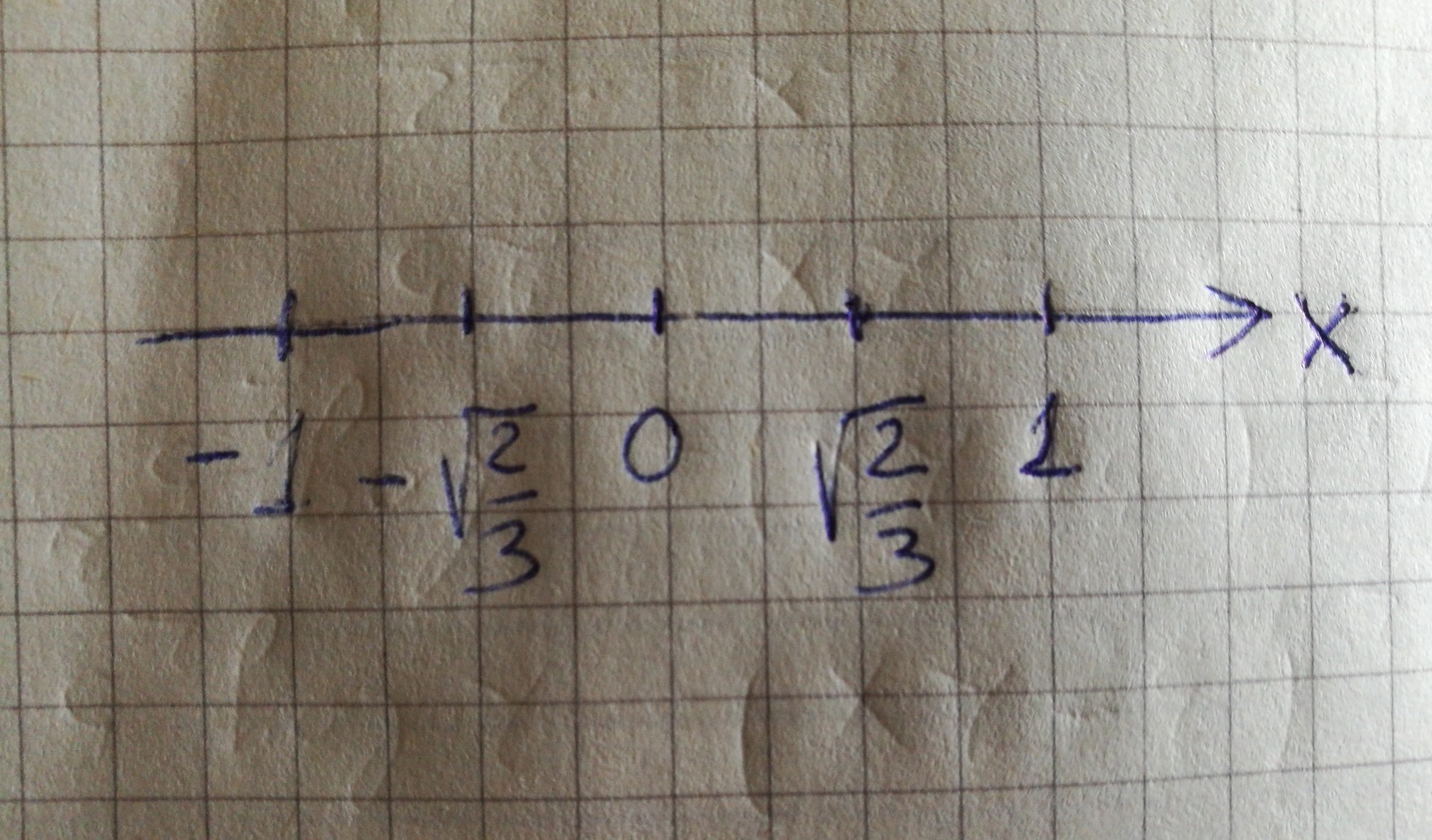
Похожие вопросы
Предмет: История,
автор: maksimsvind3
Предмет: История,
автор: feras29
Предмет: История,
автор: vladelec6479
Предмет: Обществознание,
автор: tatayanakolesnikova