Предмет: Математика,
автор: Аноним
Логарифмическое уравнение в формате ЕГЭ, подскажите как делать! Расписал ОДЗ, а вот дальше не понимаю, что надо делать!
Приложения:
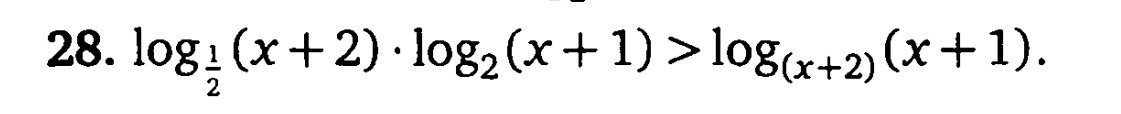
Аноним:
К основанию 2 сделать и все)
это неравенство, а не уравнение
Я не говорил что это уравнение... Неравенство можно свести к одному основанию, а именно к основанию 2. Дальше проще простого
я не вам писал, а задающему
Точно :)
Ответы
Автор ответа:
1
Самое разумное, это воспользоваться методом рационализации:
Ну и конечно, проверяем ОДЗ:
Формула написана в первой строчке
От основания отнимаем 1 и вычитаем логорифмируемые выражения (те что в скобках под логарифмом)
То есть выражение log0,5 (x+2) - log0,5 (1) перейдет в (0,5-1)*(х+2-1)
Если до сих пор не понятно, поищи в интернете: метод рационализации
Не слышал о таком
Хотя это одно и то же вроде
Похожие вопросы
Предмет: Химия,
автор: kolupaevnikita06
Предмет: Математика,
автор: anonim4709
Предмет: Українська мова,
автор: 21jimin05
Предмет: Алгебра,
автор: SEREJK
Предмет: Алгебра,
автор: fedya6886