Предмет: Алгебра,
автор: kurbonalisaido
sin^4xcos^x2x-cos^4xsin^2x=cos2x
Ответы
Автор ответа:
0
Видимо, уравнение таково:
или
решений нет
Ответ:
Приложения:
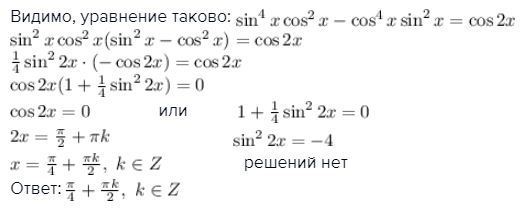
Похожие вопросы
Предмет: Математика,
автор: kisamiayr
Предмет: Математика,
автор: metaksaveronika02102
Предмет: Алгебра,
автор: mariarakelyan00
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Аноним