Question

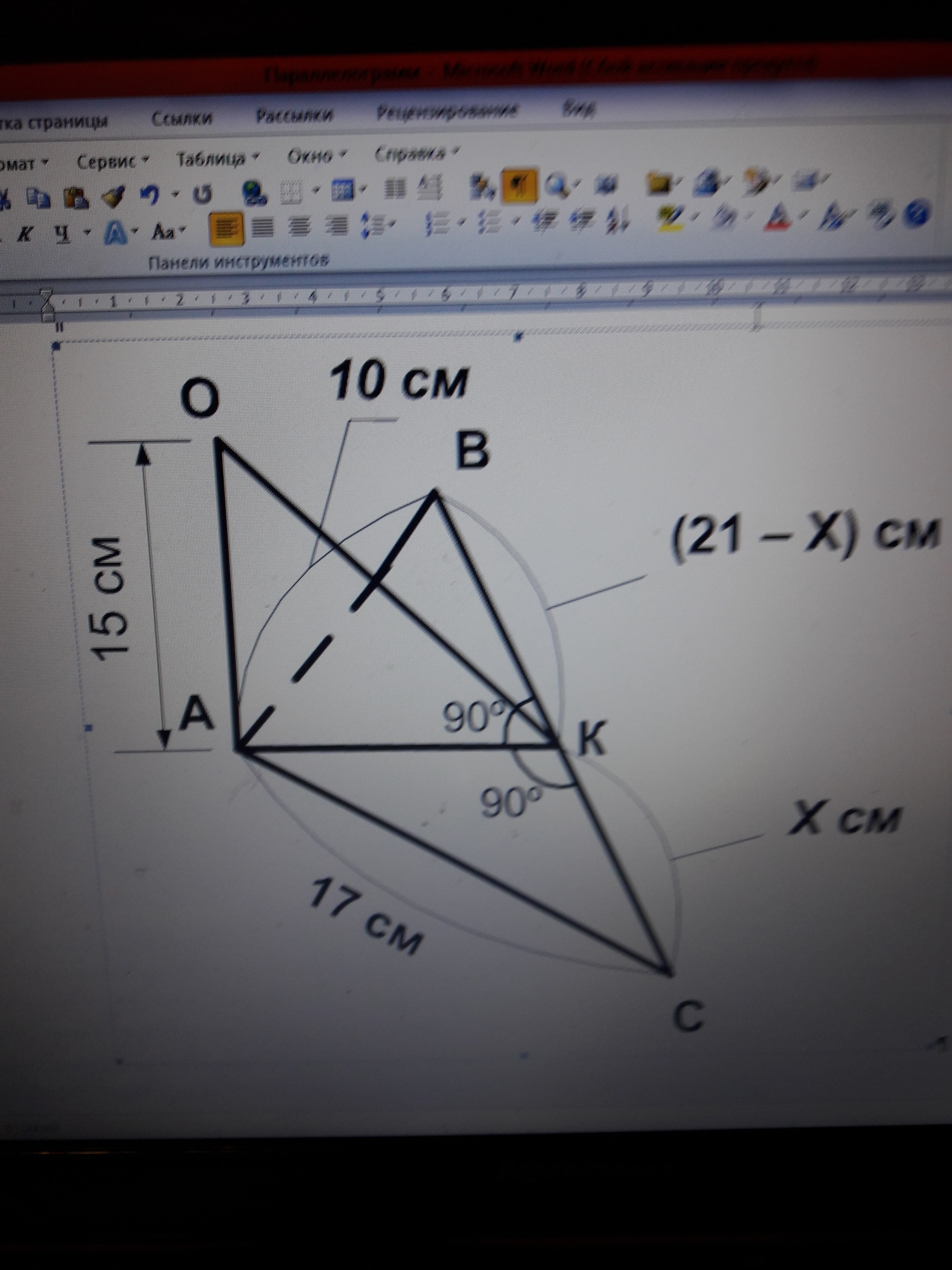
Стороны треугольника ABC: 10 см, 17 см, 21 см. Из вершины большего угла этого треугольника проведен перпендикуляр к его плоскости, равный 15 см. Определить расстояние от его концов до большей стороны.

Answer 1

Смотрим на рисунок, из треугольников АВК и АКС выражаем сторону АК:

АК² = 10² - (21 - Х)³

АК² = 17² - Х²

10² - (21 - Х)³ = 17² - Х²

100 - 441 + 42Х - Х² = 289 - Х²

42Х = 630

Х = 15 см - это расстояние от конца А перпендикуляра ОА.

ОК² = 15² + 15²= 225 + 225 = 450

ОК = √450 = √2*225= 15√2 - это расстояние от конца О перпендикуляра ОА

Ответ: 15 и 15√2