Question

в параллелограмме abcd угол а острый из вершины а проведены высоты параллелограмма am и ah к сторонам bc и cd соответсвенно,MH:AC=3:4.Найдите отношение площадей треугольников MAH и ABC

Answer 1

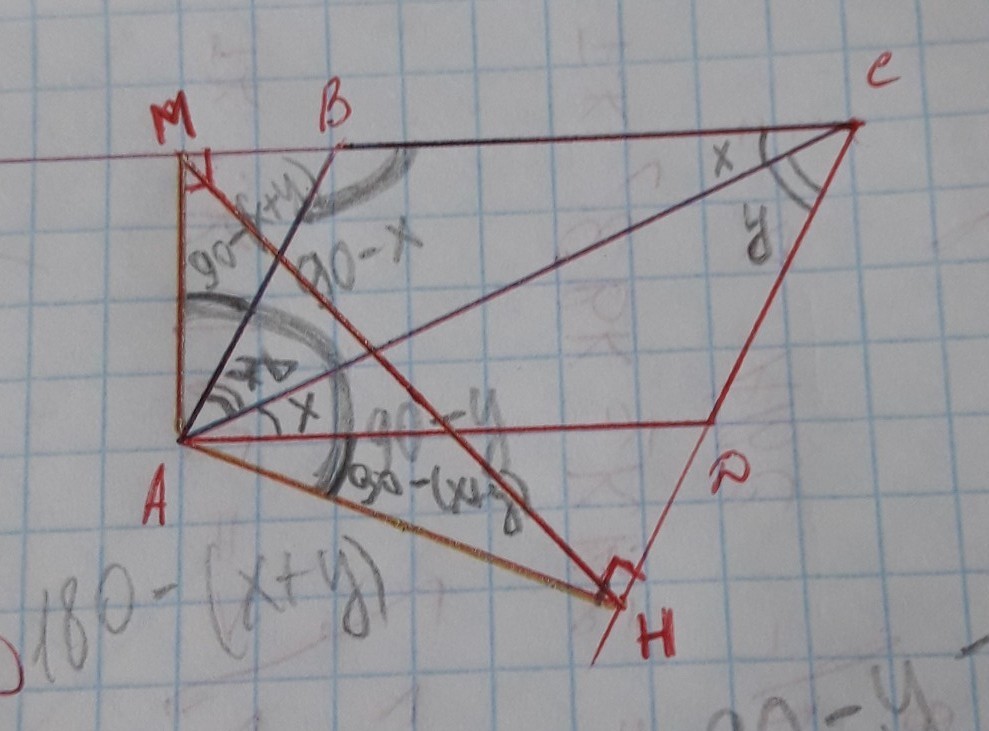
обозначим BCA=x, ACD=y.
т.к. треуг ACH прямоуг, тогда HAC=90-y.
треуг AMC прясоуг, тогда MAC=90-x.
Тогда MAH=(90-y)+(90-x)=180-(x+y).
в треуг ABC угол ABC=180-(x+y) ( т.к сумма углов в треуг 180)
т.о MAH=ABC

Рассмотрим прямоуг треуг AMB и AHD
угол HAD=HAC-CAD=90-y-x
угол MAB=MAC-BAC= 90-x-y
следовательно эти треуг подобны по двум углам ( прямые и HAD=MAB). AB:AD=AM:AH
AD=BC ( т.к параллелограмм) следовательно можно заменить AB:BC=AM:AH
т.о получаем, что треуг ABC и MAH подобны по двум сторонам и углу между ними. отношение площадей подобных треуг равно квадрату коэффициента подобия.
т.е. AM:AB=AH:BC=MH:AC=3:4. (3:4)^2= 9:16


надеюсь, не ошиблась