Предмет: Алгебра,
автор: фарт333

РЕШИТЕ ПРОИЗВОДНУЮ
matilda17562:
Обратная пропорциональность, графиком является гипербола. В чём заключается задание?
я вот сам не пойму че препод хочет
сказал решите производную
Так и нужно было сформулировать задание: "найти производную функции".
Ответы
Автор ответа:
1
_____________________________
Приложения:
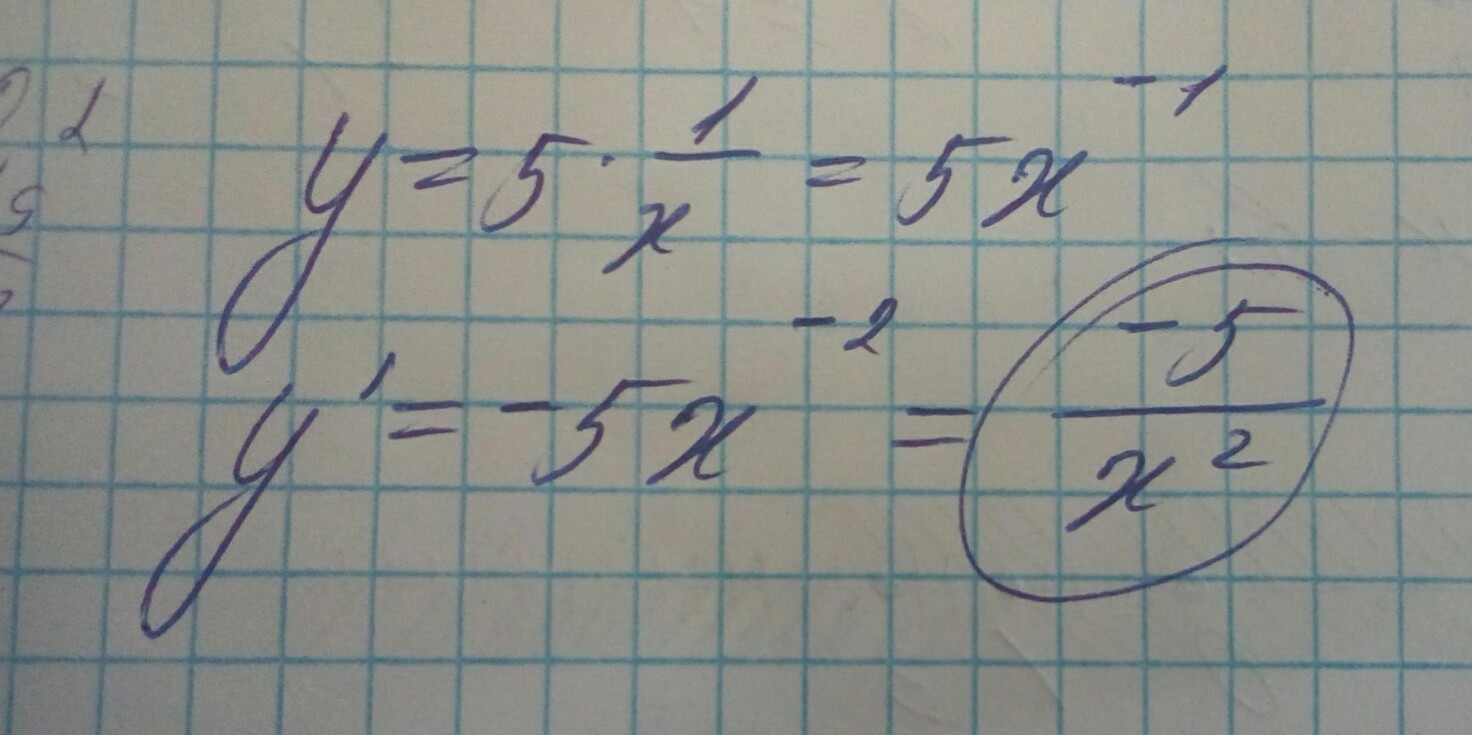
Автор ответа:
0
Решение:
у = 5х^ (-1)
у' = (5х^ (-1))' = 5• ( - 1• х^ (-2)) = -5х^(-2) = - 5/х^2.
Пояснения:
1) Постоянный множитель 5 выносим за знак производной.
2) Далее применяем правило нахождения производной степени:
(х^n)' = n• х^(n-1). В нашем случае множитель -1 выносим вперёд, а показатель степени уменьшаем на единицу, - 1• n^(- 1 - 1 ) = - 1•n^ ( -2).
3) Упрощаем получившееся выражение.
у = 5х^ (-1)
у' = (5х^ (-1))' = 5• ( - 1• х^ (-2)) = -5х^(-2) = - 5/х^2.
Пояснения:
1) Постоянный множитель 5 выносим за знак производной.
2) Далее применяем правило нахождения производной степени:
(х^n)' = n• х^(n-1). В нашем случае множитель -1 выносим вперёд, а показатель степени уменьшаем на единицу, - 1• n^(- 1 - 1 ) = - 1•n^ ( -2).
3) Упрощаем получившееся выражение.
Похожие вопросы
Предмет: Русский язык,
автор: kseniamiftahova7
Предмет: География,
автор: lifesofika90
Предмет: Математика,
автор: zvritavz
Предмет: Литература,
автор: jkmufv963
Предмет: Математика,
автор: reks15