Предмет: Алгебра,
автор: вкпа
Найти наибольшее и наименьшее значения выражения
Приложения:
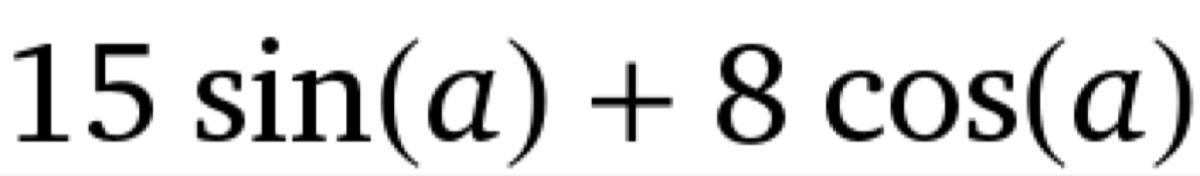
Ответы
Автор ответа:
2
По формуле вспомогательного угла
 , где
, где 

-17 - наименьшее и 17 - наибольшее
-17 - наименьшее и 17 - наибольшее
Приложения:
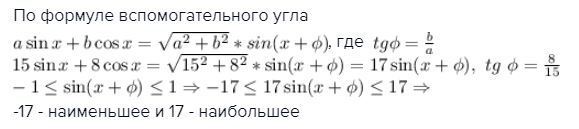
Автор ответа:
0
Решаем через вспомогательный угол.
Приложения:

Похожие вопросы
Предмет: Математика,
автор: dlapenia66667777
Предмет: Биология,
автор: anastasiagubskaa06
Предмет: Английский язык,
автор: TheDeformaZz
Предмет: Алгебра,
автор: Samisy
Предмет: Математика,
автор: lenya2004