Question

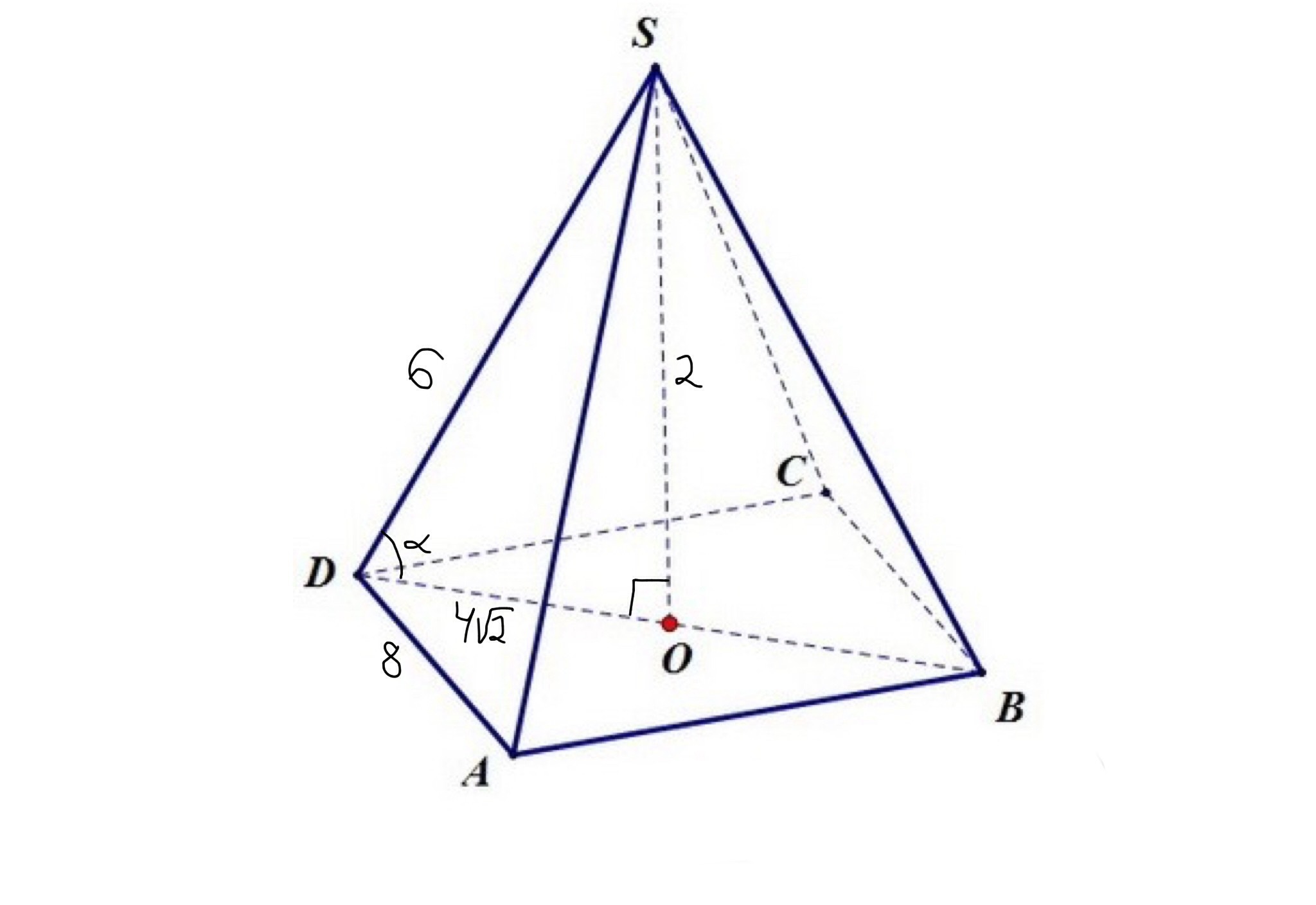
Дана правильная четырехгранная пирамида сторона основания равна 8,высота равна 2.Найти косинус угла наклона бокового ребра к основанию пирамиды?

Answer 1

Данная пирамида является правильной четырехугольной, а значит в основании лежит квадрат. Радиус окружности, описанной около квадрата, определяется по формуле:
$R=DO= \frac{a}{ \sqrt2}= \frac{8}{\sqrt2}=4\sqrt2$
Нам еще дали высоту пирамиды(SO=2), значит можно найти боковoe ребро по теореме Пифагора:
$SD= \sqrt{(4 \sqrt2)^2+2^2}= \sqrt{32+4}= \sqrt{36}=6$
Косинус равен отношению прилежащего катета к гипотенузе, то есть отношению DO к SD:
$cos \alpha= \frac{DO}{SD}= \frac{4 \sqrt{2}}{6}= \frac{2 \sqrt2}{3}$
УДАЧИ ВАМ ВО ВСЁМ)))!!!