Предмет: Алгебра,
автор: ValeraDavay
Помогите с десятым логарифмическим неравенством
Вложение
Приложения:

Ответы
Автор ответа:
0
раскладывая логарифмическое неравенство на множители, получаем

далее, используя метод рационализации (сравнивая с нулём, мы для удобства можем заменить логарифм на произведение
с нулём, мы для удобства можем заменить логарифм на произведение  при
при  ), получаем
), получаем

решив последнюю систему с помощью метода интервалов, получаем ответ:
далее, используя метод рационализации (сравнивая
решив последнюю систему с помощью метода интервалов, получаем ответ:
Автор ответа:
0
___________________________
Приложения:
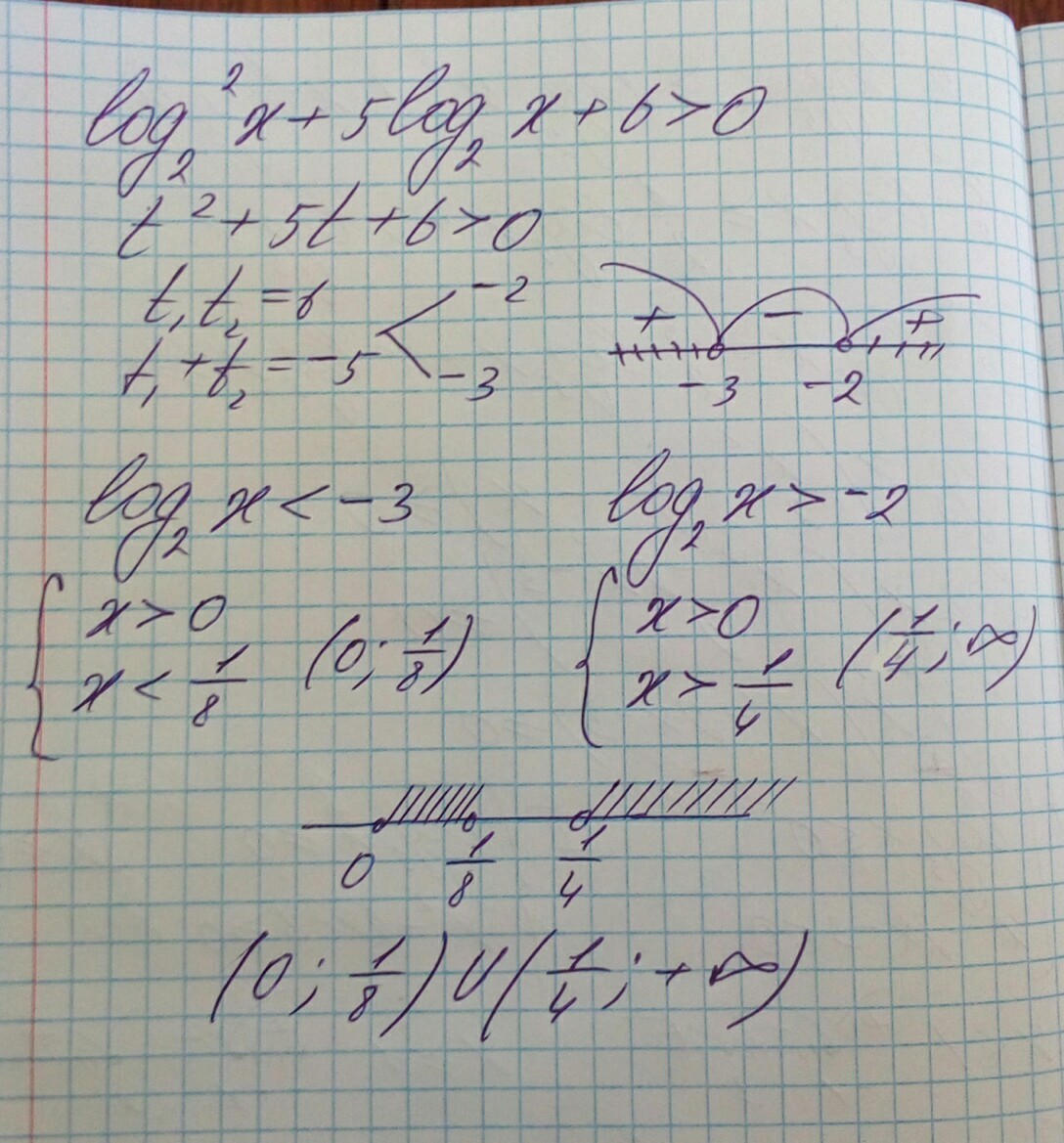
Похожие вопросы
Предмет: Немецкий язык,
автор: wow332
Предмет: Английский язык,
автор: inna323342
Предмет: Химия,
автор: lancervsaltezza
Предмет: Математика,
автор: anastasiiausha
Предмет: Физика,
автор: DashaDondokova