Предмет: Алгебра,
автор: ValeraDavay
Помогите с седьмым логарифмическим неравенством
Вложение
Приложения:
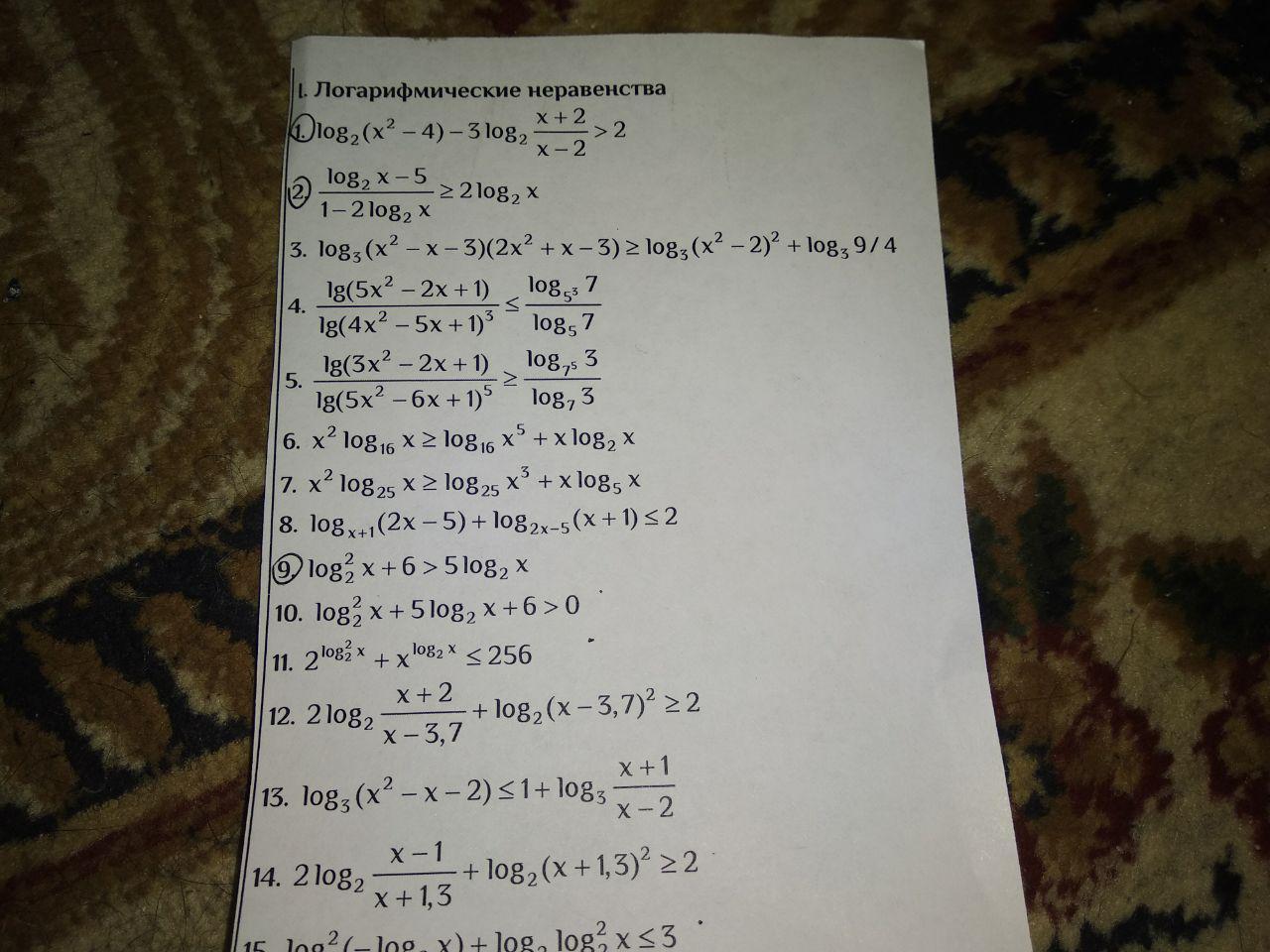
Ответы
Автор ответа:
0
7) x²log₂₅x ≥ log₂₅x³ + xlog₅x
x²log₂₅x ≥ log₂₅x³ + xlog₅x, x∈(0;+∞)
x²log₅²x ≥ log₅²x³ + xlog₅x
x²·1/2 log₅x ≥ 3/2 log₅x + xlog₅x
x²log₅x ≥ 3log₅x + 2log₅x · x
x²log₅x - 3log₅x - 2log₅x · x ≥ 0
log₅x·(x²-3-2x) ≥ 0
log₅x·(x²-2x-3) ≥ 0
log₅x·(x+1)(x-3) ≥ 0


x ≥ 1, x∈(-∞; -1]∪[3; +∞)
x ≤ 1, x∈[-1; 3]
!!! x∈(0;+∞) =>
=> x∈(0; 1]∪[3; +∞).
Ответ: x∈(0; 1]∪[3; +∞).
x²log₂₅x ≥ log₂₅x³ + xlog₅x, x∈(0;+∞)
x²log₅²x ≥ log₅²x³ + xlog₅x
x²·1/2 log₅x ≥ 3/2 log₅x + xlog₅x
x²log₅x ≥ 3log₅x + 2log₅x · x
x²log₅x - 3log₅x - 2log₅x · x ≥ 0
log₅x·(x²-3-2x) ≥ 0
log₅x·(x²-2x-3) ≥ 0
log₅x·(x+1)(x-3) ≥ 0
x ≥ 1, x∈(-∞; -1]∪[3; +∞)
x ≤ 1, x∈[-1; 3]
!!! x∈(0;+∞) =>
=> x∈(0; 1]∪[3; +∞).
Ответ: x∈(0; 1]∪[3; +∞).
Автор ответа:
0
_____________________________
Приложения:

Похожие вопросы
Предмет: Биология,
автор: sekurovavasilisa
Предмет: Українська мова,
автор: Аноним
Предмет: Физика,
автор: sergey123122
Предмет: Алгебра,
автор: ZhoraLetny