Question

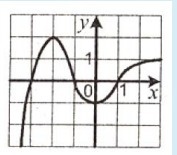
1) На рисунке изображен график функции y = f (x), определенной на множестве действительных чисел. Промежутком убывания функции является промежуток

1) -2, 0
2) -1, 2
3) -1; 1
4) -2, 1



2) График нечетной функции симметричен относительно
а) начала координат
б) оси ОХ
в) прямой у = х
г) оси ОУ

Answer 1

Задание № 1.

• Чтобы в данном случае определить промежуток убывания функции, нужно посмотреть, с какого момента значение функции начнет уменьшаться (по графику, с $x=-2$) и на каком моменте, при каком $x$, это уменьшение закончится (видно, что при $x=0$).

Получаем, что промежуток убывания функции - это $\Big [\; -2; \; 0 \; \Big ]$.

Ответ: 1).

Задание № 2.

Пусть $f(x)=y$:

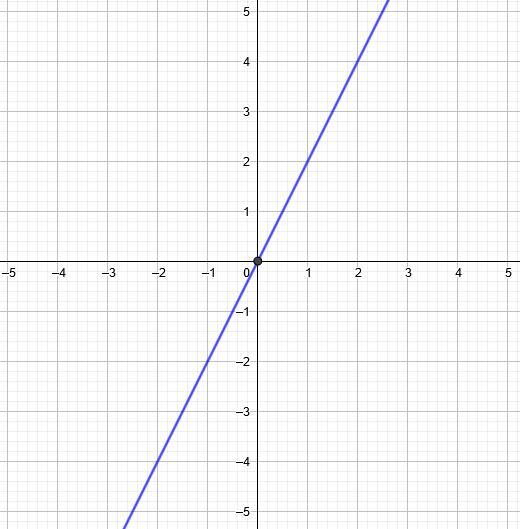
• Функция нечетная, если при подстановке в ее формулу числа $-x$ получается $-y$. Такая функция симметрична относительно начала координат. Пример - прямая пропорциональность $f(x)=2x$ (смотрите вложение 1).
• Функция четная, если при подстановке $-x$ тоже получится $y$. Такая функция симметрична относительно оси ординат. Примером может послужить парабола $f(x)=x^2$ (вложение 2).
• Если же получается что-то другое (не $y$ и не $-y$), то функция свойством четности не обладает. Пример таковой приведен в задании один.

Значит, график нечетной функции симметричен относительно начала координат (точки пересечения оси абсцисс и оси ординат).

Ответ: а).