Предмет: Алгебра,
автор: doncov2001
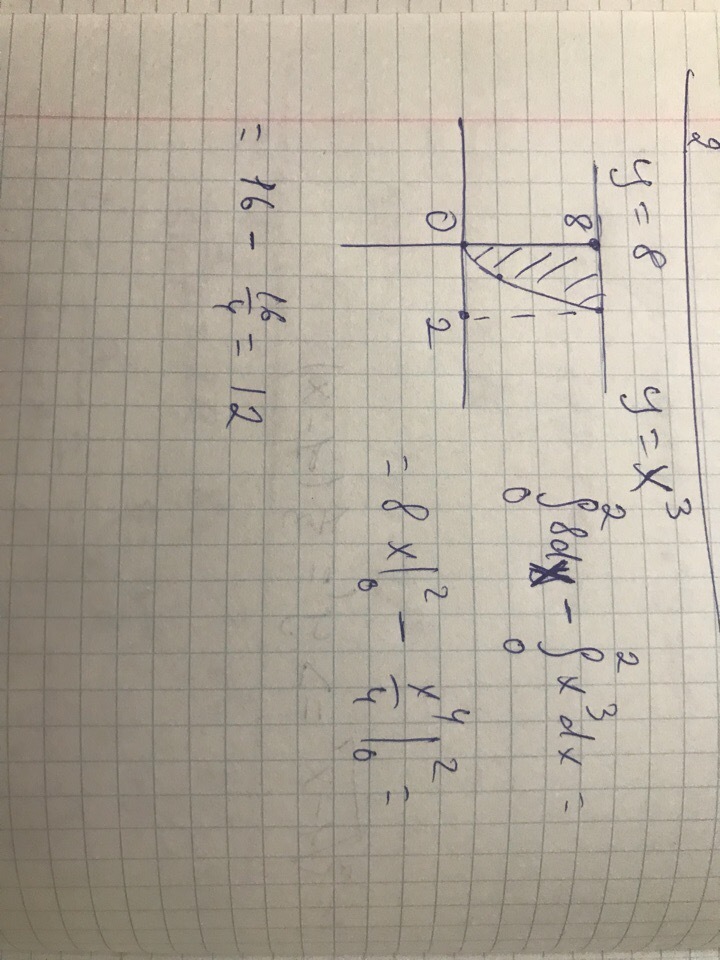
Найти площадь, ограниченную осью ординат, кубической параболой y=x^3 и прямой y=8
Ответы
Автор ответа:
0
Вроде так
Приложения:
doncov2001:
А чертеж сможешь нарисовать?Ибо ответ совпал,а чертеж не получается
Просто рисуй на точке (0;8) линию параллельную оси OX. И подставляй значения 0,1,2 в уравнение y=x^3. Получится то что тебе нужно найти то, что находится между прямой у=8 и параболой. (не тем что под параболой, а то что сверху нее). Просто тут вроде невозможно графики строить
Ты есть в вк?
примерный рисунок залил
Ну,у меня так же выходило. ХЗ првильно или нет. Ладненько,спасибо.Очень помог)
http://mathprofi.ru/vychislenie_ploshadi_c_pomoshju_opredelennogo_integrala.html
На всякий случай тут оставлю, вдруг тебе пригодится
На всякий случай тут оставлю, вдруг тебе пригодится
Угу. Спасибо
Похожие вопросы
Предмет: Биология,
автор: ymnaya89
Предмет: Обществознание,
автор: sgorbunova240
Предмет: Русский язык,
автор: khlkaterin
Предмет: Математика,
автор: марюська228
Предмет: Литература,
автор: haur